题目内容
(1)直角三角形斜边上的中线为1,周长为2+| 6 |
(2)一个三角形的三边长都是整数,周长为8,则这个三角形的面积是
(3)四边形ABCD中,∠A=60°,∠B=∠D=90°,AB=AD,AC=1,则四边形ABCD的面积是
(4)梯形ABCD中,AB∥CD,对角线AC与BD相交于O.若S△ABO=p2,S△CDO=q2,则SABCD=
(5)在△ABC中,D是AB的中点,E是AC上一点,
| AE |
| EC |
| 2 |
| 3 |
分析:(1)设直角三角形的两直角边分别等于x、y,由斜边中线的长建立方程,求解x、y的值,进而即可得出三角形的面积;
(2)由三边关系求出三边的长,再由勾股定理求出三角形的高,进而可求其面积;
(3)两个三角形全等,由边角关系求出一个三角形的面积即可;
(4)S△AOB+S△COD=S△AOD+S△BOC,即可得出梯形的面积;
(5)过点B作BG∥AE,则△ADE≌△BGD,可得S△ABE=S△BEG,再根据△DEF∽△BEG即可求解.
(2)由三边关系求出三边的长,再由勾股定理求出三角形的高,进而可求其面积;
(3)两个三角形全等,由边角关系求出一个三角形的面积即可;
(4)S△AOB+S△COD=S△AOD+S△BOC,即可得出梯形的面积;
(5)过点B作BG∥AE,则△ADE≌△BGD,可得S△ABE=S△BEG,再根据△DEF∽△BEG即可求解.
解答: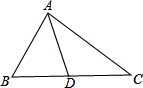 解:(1)设直角三角形的两直角边分别等于x、y,
解:(1)设直角三角形的两直角边分别等于x、y,
∵直角三角形斜边上的中线为1,
∴斜边的长=2,
∴x+y=2+
-2=
①,
∴x2+y2=4②,
解关于①②的方程,得
x=
,y=
,
或y=
,x=
,
∴S△=
xy=
×
×
=
;
(2)设这个三角形的三边是a、b、c,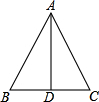
那么a+b+c=8,
又∵a、b、c是整数,a+b>c,且a、b、c均小于4,
∴a=2,b=c=3,
如右图所示,AD是底边BC上的高,AB=AC=3,
S△ABC=
BC×AD=
×2×
=2
;
(3)如右图所示,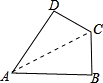
连接AC,则Rt△ACD≌Rt△ACB,
∴∠DAC=∠BAC=30°,
∵AC=1,∴CD=
,AD=
,
∴SABCD=2S△ACD=2×
×
×
=
;
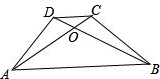
(4)如图,
∵S△AOB+S△COD=S△AOD+S△BOC,
又S△AOB=p2,S△COD=q2,
∴S梯形ABCD=2(p2+q2);
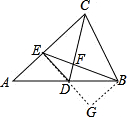
(5)如图,过点B作BG∥AE,则△ADE≌△BGD,∴S△ABE=S△BEG,
因为D为AB中点,所以D为AB中点,∴△DEF∽△BEG,
∵S△ABC=40,
=
,∴S△ABE=
×40=16,
∴S△DEF=
×16=4.
 解:(1)设直角三角形的两直角边分别等于x、y,
解:(1)设直角三角形的两直角边分别等于x、y,∵直角三角形斜边上的中线为1,
∴斜边的长=2,
∴x+y=2+
| 6 |
| 6 |
∴x2+y2=4②,
解关于①②的方程,得
x=
| ||||
| 2 |
| ||||
| 2 |
或y=
| ||||
| 2 |
| ||||
| 2 |
∴S△=
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
| 2 |
| ||||
| 2 |
| 1 |
| 2 |
(2)设这个三角形的三边是a、b、c,

那么a+b+c=8,
又∵a、b、c是整数,a+b>c,且a、b、c均小于4,
∴a=2,b=c=3,
如右图所示,AD是底边BC上的高,AB=AC=3,
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 32-12 |
| 2 |
(3)如右图所示,

连接AC,则Rt△ACD≌Rt△ACB,
∴∠DAC=∠BAC=30°,
∵AC=1,∴CD=
| 1 |
| 2 |
| ||
| 2 |
∴SABCD=2S△ACD=2×
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |

(4)如图,
∵S△AOB+S△COD=S△AOD+S△BOC,
又S△AOB=p2,S△COD=q2,
∴S梯形ABCD=2(p2+q2);

(5)如图,过点B作BG∥AE,则△ADE≌△BGD,∴S△ABE=S△BEG,
因为D为AB中点,所以D为AB中点,∴△DEF∽△BEG,
∵S△ABC=40,
| AE |
| EC |
| 2 |
| 3 |
| 2 |
| 5 |
∴S△DEF=
| 1 |
| 4 |
点评:本题考查了相似三角形的判定与性质及直角三角形的知识,难度较大,关键是掌握相似三角形的判定方法.

练习册系列答案
相关题目
若直角三角形两条直角边长分别为
cm和
cm,那么直角三角形斜边长是( )
| 15 |
| 12 |
A、3
| ||
B、3
| ||
| C、9cm | ||
| D、27cm |