题目内容
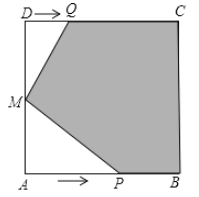
【题目】如图,在边长为12cm的正方形![]() 中,
中,![]() 是
是![]() 边的中点,点
边的中点,点![]() 从点
从点![]() 出发,在正方形边上沿
出发,在正方形边上沿![]() 的方向以大于1 cm/s的速度匀速移动,点
的方向以大于1 cm/s的速度匀速移动,点![]() 从点
从点![]() 出发,在
出发,在![]() 边上沿
边上沿![]() 方向以1 cm/s的速度匀速移动,
方向以1 cm/s的速度匀速移动,![]() 、
、![]() 两点同时出发,当点
两点同时出发,当点![]() 、
、![]() 相遇时即停止移动.设点
相遇时即停止移动.设点![]() 移动的时间为t(s),正方形
移动的时间为t(s),正方形![]() 与
与![]() 的内部重叠部分面积为
的内部重叠部分面积为![]() (cm2).已知点
(cm2).已知点![]() 移动到点
移动到点![]() 处,
处,![]() 的值为96(即此时正方形
的值为96(即此时正方形![]() 与
与![]() 的内部重叠部分面积为96cm2).
的内部重叠部分面积为96cm2).
(1)求点![]() 的速度:
的速度:
(2)求![]() 与t的函数关系式,并直接写出的取值范围.
与t的函数关系式,并直接写出的取值范围.
【答案】(1)3 cm/s;(2)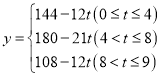 .
.
【解析】
(1)由于P的速度比Q的速度大,因此P到达B点时,Q在DC边上,此时重叠部分面积为正方形的面积减去△DQM和△ABM的面积,求解即可;
(2)分三种情况讨论:当点P在边AB上时,当点P在边BC上时,当点P在边CD上时,根据题意列函数关系式即可.
解:(1)由已知得,AB=AD=CD=BC=12,
∵M是AD边的中点,
∴AM=MD=6,
由题意可知当P到达B点时Q在DC边上,DQ=t,
∴![]() ,
,
∴![]() ,
,
解得,t=4,
∴ P点的速度为12÷4=3 cm/s;
(2)当点P在边AB上时,![]() ,
,
![]() ,
,
![]()
当点P在边BC上时,![]() ,
,
![]()
![]()
当点P在边CD上时,![]() ,
,
![]() ,
,
![]() ;
;
综上所述,y与t的函数关系式为
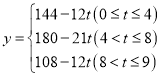 .
.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】甲、乙两名大学生竞选班长,现对甲、乙两名应聘者从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
应聘者 | 笔试 | 口试 | 得票 |
甲 | 85 | 83 | 90 |
乙 | 80 | 85 | 92 |
(1)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2:1:2来计算各人的成绩,那么又是谁会竞选上?
【题目】某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲 | 95 | 82 | 88 | 81 | 93 | 79 | 84 | 78 |
乙 | 83 | 92 | 80 | 95 | 90 | 80 | 85 | 75 |
(1)请你计算这两组数据的平均数、中位数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.