Question

【题目】如图，甲船在处发现乙船在北偏东的的处，如果此时乙船正以每小时海里的速度向正北方向行驶，而甲船的速度是海里/小时，这时甲船向________方向行驶才能最快追上乙．

Answer 1

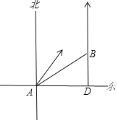
【答案】北偏东

【解析】

构建两个直角三角形后，令BD=x，则AB=2x，AD=；BC=a，则AC=a．在RT△ACD中运用勾股定理可求出a和x之间的关系，从而得到AB=BC，依据三角形外角和定理，从而求出∠CAB，又因为∠BAD已知，则可找到所行驶方向．

设甲船在C处追上乙船，根据题意知CD⊥AD，

∴∠ADB=，∠BAD=

∴AB=2BD，

由勾股定理得：AD=BD，

∵乙船正以每小时10海里的速度向正北方向行驶,而甲船的速度是10海里/小时，

∴设BC=a,则AC=a，

又在Rt△ABD中,令BD=x,则AB=2x,AD=x，

又∵在Rt△ADC中,=

∴x= (舍负)，

又在Rt△ABD中，AB=2x，

∴AB=a，

∴AB=BC，

∴∠C=∠CAB，

∴∠ABD=∠C+∠CAB，

∴∠ABD=2∠C.

∵∠ABD=

∴∠C=

∴∠CAD=

∴这时甲船应朝北偏东方向行驶，才能最快追上乙船．