题目内容
(2012•吉林)如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以A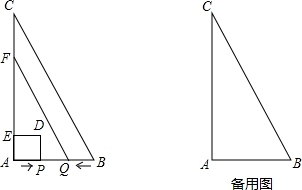 P为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
P为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
(1)当t=
(2)当t=
s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.
 P为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
P为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.(1)当t=
1
1
s时,点P与点Q重合;(2)当t=
| 4 |
| 5 |
| 4 |
| 5 |
(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.
分析:(1)当点P与点Q重合时,此时AP=BQ=t,且AP+BQ=AB=2,由此列一元一次方程求出t的值;
(2)当点D在QF上时,如答图1所示,此时AP=BQ=t.由相似三角形比例线段关系可得PQ=
t,从而由关系式AP+PQ+BQ=AB=2,列一元一次方程求出t的值;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,运动过程可以划分为两个阶段:
①当1<t≤
时,如答图3所示,此时重合部分为梯形PDGQ.先计算梯形各边长,然后利用梯形面积公式求出S;
②当
<t<2时,如答图4所示,此时重合部分为一个多边形.面积S由关系式“S=S正方形APDE-S△AQF-S△DMN”求出.
(2)当点D在QF上时,如答图1所示,此时AP=BQ=t.由相似三角形比例线段关系可得PQ=
| 1 |
| 2 |
(3)当点P在Q,B两点之间(不包括Q,B两点)时,运动过程可以划分为两个阶段:
①当1<t≤
| 4 |
| 3 |
②当
| 4 |
| 3 |
解答: 解:(1)当点P与点Q重合时,AP=BQ=t,且AP+BQ=AB=2,
解:(1)当点P与点Q重合时,AP=BQ=t,且AP+BQ=AB=2,
∴t+t=2,解得t=1s,
故填空答案:1.
(2)当点D在QF上时,如答图1所示,此时AP=BQ=t.
∵QF∥BC,APDE为正方形,∴△PQD∽△ABC,
∴DP:PQ=AC:AB=2,则PQ=
DP=
AP=
t.
由AP+PQ+BQ=AB=2,得t+
t+t=2,解得:t=
.
故填空答案:
.
(3)当P、Q重合时,由(1)知,此时t=1;
当D点在BC上时,如答图2所示,此时AP=BQ=t,BP=
t,求得t=
s,进一步分析可知此时点E与点F重合;
当点P到达B点时,此时t=2.
因此当P点在Q,B两点之间(不包括Q,B两点)时,其运动过程可分析如下:
①当1<t≤
时,如答图3所示,此时重合部分为梯形PDGQ.
此时AP=BQ=t,∴AQ=2-t,PQ=AP-AQ=2t-2;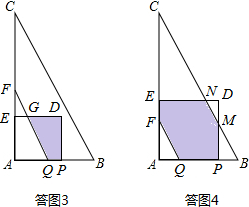
易知△ABC∽△AQF,可得AF=2AQ,EF=2EG.
∴EF=AF-AE=2(2-t)-t=4-3t,EG=
EF=2-
t,
∴DG=DE-EG=t-(2-
t)=
t-2.
S=S梯形PDGQ=
(PQ+DG)•PD,
=
[(2t-2)+(
t-2)]•t,
=
t2-2t;
②当
<t<2时,如答图4所示,此时重合部分为一个多边形.
此时AP=BQ=t,∴AQ=PB=2-t,
易知△ABC∽△AQF∽△PBM∽△DNM,可得AF=2AQ,PM=2PB,DM=2DN,
∴AF=4-2t,PM=4-2t.
又∵DM=DP-PM=t-(4-2t)=3t-4,
∴DN=
(3t-4)=
t-2,DM=3t-4.
S=S正方形APDE-S△AQF-S△DMN=AP2-
AQ•AF-
DN•DM
=t2-
(2-t)(4-2t)-
×
(3t-4)×(3t-4)
=-
t2+10t-8.
综上所述,当点P在Q,B两点之间(不包括Q,B两点)时,S与t之间的函数关系式为:
S=
.
 解:(1)当点P与点Q重合时,AP=BQ=t,且AP+BQ=AB=2,
解:(1)当点P与点Q重合时,AP=BQ=t,且AP+BQ=AB=2,∴t+t=2,解得t=1s,
故填空答案:1.
(2)当点D在QF上时,如答图1所示,此时AP=BQ=t.
∵QF∥BC,APDE为正方形,∴△PQD∽△ABC,
∴DP:PQ=AC:AB=2,则PQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由AP+PQ+BQ=AB=2,得t+
| 1 |
| 2 |
| 4 |
| 5 |
故填空答案:
| 4 |
| 5 |
(3)当P、Q重合时,由(1)知,此时t=1;
当D点在BC上时,如答图2所示,此时AP=BQ=t,BP=
| 1 |
| 2 |
| 4 |
| 3 |
当点P到达B点时,此时t=2.
因此当P点在Q,B两点之间(不包括Q,B两点)时,其运动过程可分析如下:
①当1<t≤
| 4 |
| 3 |
此时AP=BQ=t,∴AQ=2-t,PQ=AP-AQ=2t-2;

易知△ABC∽△AQF,可得AF=2AQ,EF=2EG.
∴EF=AF-AE=2(2-t)-t=4-3t,EG=
| 1 |
| 2 |
| 3 |
| 2 |
∴DG=DE-EG=t-(2-
| 3 |
| 2 |
| 5 |
| 2 |
S=S梯形PDGQ=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 5 |
| 2 |
=
| 9 |
| 4 |
②当
| 4 |
| 3 |
此时AP=BQ=t,∴AQ=PB=2-t,
易知△ABC∽△AQF∽△PBM∽△DNM,可得AF=2AQ,PM=2PB,DM=2DN,
∴AF=4-2t,PM=4-2t.
又∵DM=DP-PM=t-(4-2t)=3t-4,
∴DN=
| 1 |
| 2 |
| 3 |
| 2 |
S=S正方形APDE-S△AQF-S△DMN=AP2-
| 1 |
| 2 |
| 1 |
| 2 |
=t2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 9 |
| 4 |
综上所述,当点P在Q,B两点之间(不包括Q,B两点)时,S与t之间的函数关系式为:
S=
|
点评:本题是运动型综合题,涉及到动点与动线问题.第(1)(2)问均涉及动点问题,列方程即可求出t的值;第(3)问涉及动线问题,是本题难点所在,首先要正确分析动线运动过程,然后再正确计算其对应的面积S.本题难度较大,需要同学们具备良好的空间想象能力和较强的逻辑推理能力.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
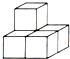 (2012•吉林)如图,有5个完全相同的小正方体组合成一个立方体图形,它的俯视图是( )
(2012•吉林)如图,有5个完全相同的小正方体组合成一个立方体图形,它的俯视图是( ) (2012•吉林)如图,在△ABC中,∠A=80°,∠B=40°.D、E分别是AB,AC上的点,且DE∥BC,则∠AED的度数是( )
(2012•吉林)如图,在△ABC中,∠A=80°,∠B=40°.D、E分别是AB,AC上的点,且DE∥BC,则∠AED的度数是( )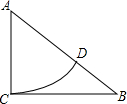 (2012•吉林)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=
(2012•吉林)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=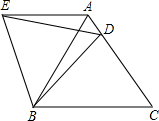 (2012•吉林)如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是
(2012•吉林)如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是