��Ŀ����
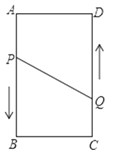
����Ŀ����������AMFN�У���AMΪBC���ϵĸ����ȱ�������ABC����AB�Ƶ�A��ʱ����ת90������D��D��ǡ������NF�ϣ�����BD��AC��BD���ڵ�E������CD.
(1)��ͼ1����֤����AMC�ա�AND��
(2)��ͼ1����DF=![]() ����AE�ij���
����AE�ij���
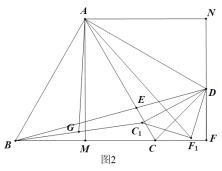
(3)��ͼ2,����CDF�Ƶ�D˳ʱ����ת![]() ��
��![]() ��,��C,F�Ķ�Ӧ��ֱ�Ϊ
��,��C,F�Ķ�Ӧ��ֱ�Ϊ![]() ��
��![]() .����
.����![]() ��
��![]() ����G��
����G��![]() ���е�,����AG.��̽��
���е�,����AG.��̽��![]() �Ƿ�Ϊ��ֵ�����Ƕ�ֵ���������ֵ�������ǣ���˵������.
�Ƿ�Ϊ��ֵ�����Ƕ�ֵ���������ֵ�������ǣ���˵������.

���𰸡���1������������2��AE��![]() ����3����3��
����3����3��![]() �����ɼ�����.
�����ɼ�����.
��������
��1�������ı���AMFN�������εõ��жϡ�AMC,��AND��Rt������һ��˵����ABC�ǵȱ������Σ��ڽ����ת�����ʣ�����֤��.
��2����E��EG��AB��G,��BC��һ��H������DH,ʹBH=HD����AG��![]() ����AE=
����AE=![]() GE=
GE=![]() ���õ���GBE�ǵ���ֱ�������κ͡�DHF=30�����ٽ��ֱ�������ε����ʣ��ж�Rt��AMC��Rt��AND�����ͨ���������AE�ij���
���õ���GBE�ǵ���ֱ�������κ͡�DHF=30�����ٽ��ֱ�������ε����ʣ��ж�Rt��AMC��Rt��AND�����ͨ���������AE�ij���
��3���ӳ�F1G��M,�ӳ�BA��![]() ���ӳ�����N,ʹ��
���ӳ�����N,ʹ��![]() ���ɵ�
���ɵ�![]() ��
��![]() ���Ӷ��õ�
���Ӷ��õ�![]()
![]() ����֪
����֪![]() ��
��![]() ,�ٸ�������֤��
,�ٸ�������֤��![]() ��
��![]() ����һ��˵��
����һ��˵��![]() �ǵ���ֱ�������Σ�Ȼ����ʹ�ù��ɶ�����⼴��.
�ǵ���ֱ�������Σ�Ȼ����ʹ�ù��ɶ�����⼴��.
��1��֤�������ı���AMFN�������Σ�
��AM=AN ��AMC=��N=90��
���AMC,��AND��Rt��
�ߡ�ABC�ǵȱ�������
��AB=AC
����ת��AB=AD
��AC=AD
��Rt��AMC��Rt��AND(HL)
��2����E��EG��AB��G,��BC��һ��H������DH,ʹBH=HD��

��AG��![]()
��AE=![]() GE=
GE=![]()
����GBE�ǵ���ֱ��������
��BG=EG��![]()
��AB=BC=![]()
�á�DHF=30��
��HD=2DF=![]() HF=
HF=![]()
��BF=BH+HF=![]()
��Rt��AMC��Rt��AND(HL)
����CF=DF=![]()
��BC=BF-CF=![]()
��![]()
��![]()
��AE��![]()
��3��![]() ��
��
���ɣ���ͼ2��,�ӳ�F1G��M,�ӳ�BA��![]() ���ӳ�����N,ʹ��
���ӳ�����N,ʹ��![]() ,��
,��![]() ��
��![]() ,
,

��![]()
![]() ,
,
��![]() ��
��![]() ,
,
��![]()
��![]()
![]()
��![]()
��![]() ,
,
��![]()
��![]() ��
��![]() ��SAS��
��SAS��
��![]()
![]()
��![]()
��![]() �ǵ���ֱ��������
�ǵ���ֱ��������
��![]()
![]()
��![]()
��![]()