题目内容
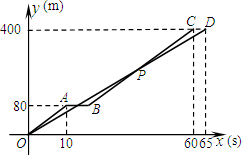 (2013•沙河口区一模)在校运动会男子400m比赛中,甲乙两名运动员同时起跑.刚跑出80m,甲不慎摔倒,他迅速地爬起来并按原速度再次投入比赛,最终取得了优异的成绩.如图分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系(假设他们跑步时都是匀速的).根据图象解答下列问题:
(2013•沙河口区一模)在校运动会男子400m比赛中,甲乙两名运动员同时起跑.刚跑出80m,甲不慎摔倒,他迅速地爬起来并按原速度再次投入比赛,最终取得了优异的成绩.如图分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系(假设他们跑步时都是匀速的).根据图象解答下列问题:(1)图中线段OA表示的是
甲
甲
(填“甲”或填“乙”)所跑的路程与比赛时间之间的关系;(2)求甲跑步的速度;
(3)甲再次投入比赛后,在距离终点多远处追上乙?
分析:(1)通过分析函数图象就可以得出OA段图象表示的意义;
(2)由函数图象可以看出甲10秒跑的路程式80米,可以由速度=路程÷时间而的结论;
(3)先求出点B的坐标,求出BC和OD的解析式,根据一次函数与二元一次方程组的关系就可以求出结论.
(2)由函数图象可以看出甲10秒跑的路程式80米,可以由速度=路程÷时间而的结论;
(3)先求出点B的坐标,求出BC和OD的解析式,根据一次函数与二元一次方程组的关系就可以求出结论.
解答:解:(1)由函数图象得线段OA表示的是甲跑的路程与时间之间的关系;
(2)由函数图象,得
80÷10=8米/秒.
答:甲跑步的速度为8米/秒;
(3)由图象及甲的速度可以求出甲不摔倒跑完全程的时间为:400÷8=50秒,
∴甲摔倒耽误的时间为:60-50=10秒,
∴B(20,80).
设直线BC的解析式为:y1=k1x+b1,设直线OD的解析式为y2=k2x,由图象,得
,400=65k2,
解得:
,k2=
,
∴直线BC的解析式为:y1=8x-80,直线OD的解析式为:y2=
x,
当y1=y2时,8x-80=
x,
解得:x=
.
∴相遇时离终点的距离为:400-
×
=
米.
答:甲再次投入比赛后,在距离终点
米处追上乙.
故答案为:甲.
(2)由函数图象,得
80÷10=8米/秒.
答:甲跑步的速度为8米/秒;
(3)由图象及甲的速度可以求出甲不摔倒跑完全程的时间为:400÷8=50秒,
∴甲摔倒耽误的时间为:60-50=10秒,
∴B(20,80).
设直线BC的解析式为:y1=k1x+b1,设直线OD的解析式为y2=k2x,由图象,得
|
解得:
|
| 80 |
| 13 |
∴直线BC的解析式为:y1=8x-80,直线OD的解析式为:y2=
| 80 |
| 13 |
当y1=y2时,8x-80=
| 80 |
| 13 |
解得:x=
| 130 |
| 3 |
∴相遇时离终点的距离为:400-
| 80 |
| 13 |
| 130 |
| 3 |
| 400 |
| 3 |
答:甲再次投入比赛后,在距离终点
| 400 |
| 3 |
故答案为:甲.
点评:本题是一道一次函数的综合试题,考查了对函数图象理解的运用,行程问题的数量关系的运用,待定系数法求一次函数的解析式的运用,解答第三问时求出函数的解析式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
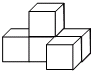 (2013•沙河口区一模)如图是由5个大小相同的正方体组成的几何体,它的俯视图是( )
(2013•沙河口区一模)如图是由5个大小相同的正方体组成的几何体,它的俯视图是( )