题目内容
如图，矩形
的两条对角线相交于点
，
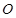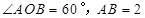，则矩形的边长
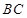的长是（ ）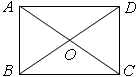
| A．2 | B．4 | C． | D． |
C
解析试题分析：根据矩形的性质结合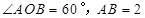，可得△ABO为等边三角形，即可得到对角线AC的长，再根据勾股定理即可求得结果.
∵矩形，
∴
，
，
，
∴
，
∵，
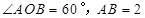∴△ABO为等边三角形，
∴
，
∴
，
∴
，
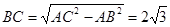故选C.
考点：本题考查的是矩形的性质，勾股定理，等边三角形的判定和性质
点评：解答本题的关键是熟练掌握矩形的对角线相等且互相平分，有一个角是60°的等腰三角形是等边三角形.
练习册系列答案
相关题目
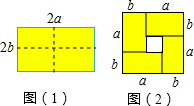如图（1），是一个长为2a宽为2b（a＞b）的矩形，用剪刀沿矩形的两条对角轴剪开，把它分成四个全等的小矩形，然后按图（2）拼成一个新的正方形，则中间空白部分的面积是（ ）| A、ab | B、（a+b）2 | C、（a-b）2 | D、a2-b2 |
，高为________cm．
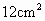，一边与一条对角线的比为3∶5，则矩形的对角线长是________cm．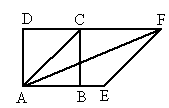
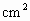，高为________cm．
，一边与一条对角线的比为3∶5，则矩形的对角线长是________cm．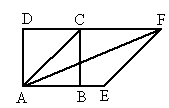
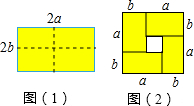如图（1），是一个长为2a宽为2b（a＞b）的矩形，用剪刀沿矩形的两条对角轴剪开，把它分成四个全等的小矩形，然后按图（2）拼成一个新的正方形，则中间空白部分的面积是