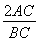题目内容
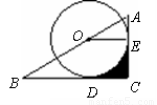
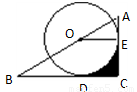
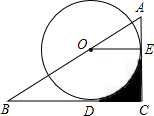 如图,点O在Rt△ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连接OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么
如图,点O在Rt△ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连接OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么| BC |
| AC |
| A、2.7 | B、2.5 |
| C、2.3 | D、2.1 |
分析:如图,连接OD,则四边形OECD是正方形,根据题意知道S阴影部分=S正方形OECD-S扇形ODE=OE2-
πOE2,S△AEO=
OE•AE,而OE∥CB,由此即可取出
的值.
| 1 |
| 4 |
| 1 |
| 2 |
| BC |
| AC |
解答: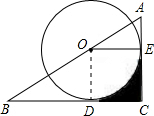 解:如图,连接OD,
解:如图,连接OD,
∵⊙O切AC边于点E,切BC边于点D,
∴∠ODC=∠OEC=∠C=90°,
∴四边形OECD是正方形,
而S阴影部分=S正方形OECD-S扇形ODE=OE2-
πOE2=S△AEO=
OE•AE,
∴OE:AE=
:(1-
),
∵OE∥BC,
∴
=
=
:(1-
)≈2.3.
故选C.
 解:如图,连接OD,
解:如图,连接OD,∵⊙O切AC边于点E,切BC边于点D,
∴∠ODC=∠OEC=∠C=90°,
∴四边形OECD是正方形,
而S阴影部分=S正方形OECD-S扇形ODE=OE2-
| 1 |
| 4 |
| 1 |
| 2 |
∴OE:AE=
| 1 |
| 2 |
| π |
| 4 |
∵OE∥BC,
∴
| BC |
| AC |
| OE |
| AE |
| 1 |
| 2 |
| π |
| 4 |
故选C.
点评:此题主要考查正方形的判定和性质,扇形的面积公式,直角三角形的面积公式,平行线的性质,综合性强;但题型常规,图形较熟悉,而有些学生不会添辅线导致不能解题.

练习册系列答案
相关题目
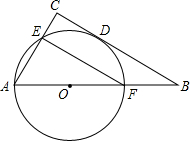 (2012•南湖区二模)如图,点O在Rt△ABC的斜边AB上,以O为圆心,OA长为半径的⊙O切BC于点D,且分别交AC、AB于点E、F,若AC=6,BC=6
(2012•南湖区二模)如图,点O在Rt△ABC的斜边AB上,以O为圆心,OA长为半径的⊙O切BC于点D,且分别交AC、AB于点E、F,若AC=6,BC=6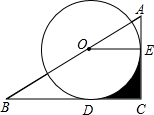 如图,点O在Rt△ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连接OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么
如图,点O在Rt△ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连接OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么