��Ŀ����
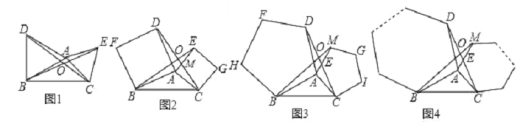
����Ŀ����ͼ1��2��3�ֱ�����ABC��AB��ACΪ������ABC�����������Σ��ȱ������Σ������ı��Σ������Σ���������Σ�BE��CD�ཻ�ڵ�O��

��1����ͼ1�У���֤����ABE�ա�ADC��
��2���ɣ�1��֤����ABE�ա�ADC���ɴ˿��Ƶ���ͼ1����BOC=120�㣬����̽����ͼ2�У���BOC�Ķ�������˵�����ɻ�д��֤�����̣�
��3����գ���������1����2���Ļ����Ͽɵ���ͼ3����BOC= ����д��������
��4���ɴ��ƹ㵽һ�����Σ���ͼ4�����ֱ�����ABC��AB��ACΪ������ABC������n���Σ�BE��CD���ཻ�ڵ�O���������BOC�Ķ���Ϊ ���ú�n��ʽ�ӱ�ʾ����
���𰸡�(1)�����������2����BOC=90�㣬���ɼ���������3��72�㣻��4����BOC�Ķ���Ϊ![]() ������������.
������������.
��������
�����������1�����ݵȱ�������֤��AB=AD��AC=AE�������õ�ʽ���ʵ���DAC=��BAE������SAS�ó���ABE�ա�ADC����2����������������֤����ABE�ա�ADC������BEA=��DCA������������ACEG���ڽ���EAC=90�����������ǺͶ�������BOC=90�㣻��3������������ε�����֤������ADC�ա�ABM���ټ��������ÿһ���ڽǵĶ���Ϊ108�㣬����������Ƕ��������BOC=72�㣻��4��������n���ε�����֤������ADC�ա�ABM���ټ���n����ÿһ���ڽǵĶ���Ϊ180�㩁![]() ������������Ƕ��������BOC=
������������Ƕ��������BOC=![]() ��
��
�����������1����ͼ1���ߡ�ABD����ACE�ǵȱ������Σ�
��AB=AD��AC=AE����DAB=��EAC=60�㣬
���DAB+��BAC=��EAC+��BAC��
����DAC=��BAE��
���ABE�ա�ADC��
��2����ͼ2����BOC=90�㣬�����ǣ�
���ı���ABFD���ı���ACGE���������Σ�
��AB=AD��AC=AE����DAB=��EAC=90�㣬
���BAE=��DAC��
���ADC�ա�ABE��
���BEA=��DCA��
�ߡ�EAC=90�㣬
���AMC+��DCA=90�㣬
�ߡ�BOC=��OME+��BEA=��AMC+��DCA��
���BOC=90�㣻
��3����ͼ3��ͬ���ã���ADC�ա�ABM��
���BME=��DCA��
�ߡ�BOC=��BME+��OEM=��DCA+��AEC��
���������ACIGM��
���EAC=180�㩁![]() =108�㣬
=108�㣬
���DCA+��AEC=72�㣬
���BOC=72�㣻
��4����ͼ4����BOC�Ķ���Ϊ![]() �������ǣ�
�������ǣ�
ͬ���ã���ADC�ա�ABM��
���BME=��DCA��
�ߡ�BOC=��BME+��OEM=��DCA+��AEC��
����n����AC��M��
���EAC=180�㩁![]() ��
��
���DCA+��AEC=180�㩁��180�㩁![]() ��
��
���BOC=![]() ��
��

 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�