题目内容
如图，在?ABCD中，E在AB上，CE、BD交于F，若AE：BE=4：3，且BF=2，则DF=
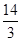
试题分析：由四边形ABCD是平行四边形，可得AB∥CD，AB=CD，继而可判定△BEF∽△DCF，根据相似三角形的对应边成比例，即可得BF：DF=BE：CD问题得解．
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∵AE：BE=4：3，
∴BE：AB=3：7，
∴BE：CD=3：7．
∵AB∥CD，
∴△BEF∽△DCF，
∴BF：DF=BE：CD=3：7，
即2：DF=3：7，
∴DF=
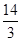．考点: （1）相似三角形的判定与性质；（2）平行四边形的性质．
练习册系列答案
相关题目
的值 .
为
，为了提高河坝的抗洪能力，防汛指挥部决定加固河坝，若坝顶CD加宽0.8米，新的背水坡EF的坡度为1：1.4．河坝总长度为500米．
=DM·EN
的值；