��Ŀ����
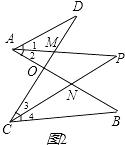
����Ŀ����֪����ͼ1���߶�AB��CD�ཻ�ڵ�O������AD��CB�����ǰ�����ͼ1��ͼ�γ�֮Ϊ��8���Ρ����Խ���������⣺ 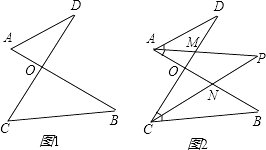
��1����ͼ1�У���ֱ��д����A����B����C����D֮���������ϵ��
��2����ͼ2�У�����D=40�㣬��B=36�㣬��DAB�͡�BCD��ƽ����AP��CP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ��M��N�����ã�1���Ľ��ۣ������P�Ķ�����
��3�����ͼ2�С�D�͡�BΪ�����ʱ�������������䣬���ʡ�P���D����B֮�������������������ϵ����˵�����ɣ�
���𰸡�
��1����A+��D=��C+��B
��2���⣺�ɣ�1����֪����1+��D=��P+��3����
��4+��B=��2+��P����
�ߡ�DAB�͡�BCD��ƽ����AP��CP�ཻ�ڵ�P��
���1=��2����3=��4��
�ɢ�+�ڵã���1+��D+��4+��B=��P+��3+��2+��P��
��2��P=��D+��B��
�֡ߡ�D=40�㣬��B=36�㣬
��2��P=40��+36��=76�㣬
���P=38��
��3���⣺��P���D����B֮����ڵĹ�ϵΪ2��P=��D+��B��
�ߡ�1+��D=��P+��3����
��4+��B=��2+��P����
�ߡ�DAB�͡�BCD��ƽ����AP��CP�ཻ�ڵ�P��
���1=��2����3=��4��
�ɢ�+�ڵã���1+��D+��4+��B=��P+��3+��2+��P��
��2��P=��D+��B��
���������⣺��1�������������ڽǺͶ����Լ��Զ�����ȣ��ɵý��ۣ���A+��D=��C+��B�����Դ��ǣ���A+��D=��C+��B��
�����㾫�������������ε��ڽǺ���Ǻ������ε�����ǽ����ĸ�������Ҫ֪�������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�������һ������һ�ߵ��ӳ�����ɵĽǣ��������ε���ǣ������ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�