题目内容
【题目】我们可以用几何图形来解决一些代数问题,如图(甲)可以来解释(a+b)2=a2+2ab+b2,
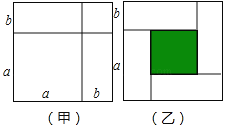
(1)图(乙)是四张全等的矩形纸片拼成的图形,请利用图中阴影部分面积的不同表示方法,写出一个关于a,b代数恒等式表示 ;
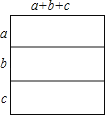
(2)请构图解释:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(3)请通过构图因式分解:a2+3ab+2b2.
【答案】(1)(a﹣b)2=(a+b)2﹣4ab.
(2)
(3)a2+3ab+2b2=(a+2b)(a+b)
【解析】
试题分析:(1)根据阴影部分的两种面积表示形式可得出恒等式.
(2)正方形的面积等于边长的平方可构建一个边长为a+b+c的正方形来验证等式.
(3)可通过构建长方形,利用长方形的面积来验证等式.
解:(1)阴影部分的边长为(a﹣b),
∴(a﹣b)2=(a+b)2﹣4ab.
(2)

(a+b+c)2=a(a+b+c)+b(a+b+c)+c(a+b+c)=a2+b2+c2+2ab+2bc+2ac.
(3)
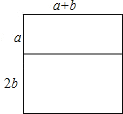
(a+2b)(a+b)=a(a+b)+2b(a+b),
∴可得a2+3ab+2b2=(a+2b)(a+b).

【题目】某社区青年志愿者小分队年龄情况如表所示:
年龄(岁) | 18 | 19 | 20 | 21 | 22 |
人数 | 2 | 5 | 2 | 2 | 1 |
则这12名队员年龄的众数、中位数分别是( )
A.2,20岁
B.2,19岁
C.19岁,20岁
D.19岁,19岁
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | 200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.