题目内容
如图10所示,Rt△ABC是一张放在平面直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
(1)在图10所示的直角坐标系中,求E点的坐标及AE的长。
(2)线段AD上有一动点P(不与A、D重合)自A点沿AD方向以每秒1个单位长度向D点作匀速运动,设运动时间为t秒(0<t<3),过P点作PM∥DE交AE于M点,过点M作MN∥AD交DE于N点,求四边形PMND的面积S与时间t之间的函数关系式,当t取何值时,S有最大值?最大值是多少?
(3)当t(0<t<3)为何值时,A、D、M三点构成等腰三角形?并求出点M的坐标。

图10
解(1)

据题意,△AOE≌△ADE
∴OE=DE,∠ADE=∠AOE=900,AD=AO=3
在Rt△AOB中,
![]()
设DE=OE=x
在Rt△BED中
BD2+DE2=BE2
即22+x2=(4-x)2
解得![]()
∴E(0,![]() )
)
在Rt△AOE中
![]()
(2)∵PM∥DE,MN∥AD,且∠ADE=900
∴四边形PMND是矩形
∵AP=t×1=t
∴PD=3-t
∵△AMP∽△AED
∴![]()
∴PM=![]()
∴![]()
∴![]() 或
或![]()
当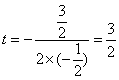 时
时
![]()
(3)△ADM为等腰三角形有以下二种情况
①当MD=MA时,点P是AD中点

∴![]()
∴![]() (秒)
(秒)
∴当![]() 时,A、D、M三点构成等腰三角形
时,A、D、M三点构成等腰三角形
过点M作MF⊥OA于F
∵△APM≌△AFM
∴AF=AP=![]() ,MF=MP=
,MF=MP=![]()
∴OF=OA-AF=3-![]()
∴M(![]() ,
,![]() )
)
②当AD=AM=3时

△AMP∽△AED
∴![]()
∴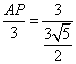
∴![]()
∴![]() (秒)
(秒)
∴当![]() 秒时,A、D、M三点构成等腰三角形
秒时,A、D、M三点构成等腰三角形
过点M作MF⊥OA于F
∵△AMF≌△AMP
∴AF=AP=![]() ,FM=PM=
,FM=PM=![]()
∴OF=OA-AF=3-![]()
∴M(![]() ,
,![]() )
)

 学校围墙边有一个直角三角形的花圃(如图1所示的Rt△ABC),其中斜边AB借助围墙,两条直角边AC和BC用铁栅栏围成,已知AB=10米,AC=8米.
学校围墙边有一个直角三角形的花圃(如图1所示的Rt△ABC),其中斜边AB借助围墙,两条直角边AC和BC用铁栅栏围成,已知AB=10米,AC=8米.

