题目内容
 已知:如图,B′A⊥AB,C′A⊥AC,AB′=AB,AC′=AC.求证:BC=B′C′.
已知:如图,B′A⊥AB,C′A⊥AC,AB′=AB,AC′=AC.求证:BC=B′C′.
证明:∵B′A⊥AB,C′A⊥AC,
∴∠C′AC=∠B′AB=90°,
∴∠C′AC+∠CAB′=∠BAB′+∠CAB′,
即∠C′AB′=∠CAB,
在△C′AB′和△CAB中,AC′=AC,∠C′AB′=∠CAB,AB′=AB,
∴△C′AB′≌△CAB,
∴BC=B′C′.
分析:求出∠C′AC=∠B′AB=90°,推出∠C′AB′=∠CAB,根据SAS证出△C′AB′≌△CAB即可.
点评:本题考查了全等三角形的性质和判定的应用,关键是证出△C′AB′≌△CAB,题型较好,难度适中.
∴∠C′AC=∠B′AB=90°,
∴∠C′AC+∠CAB′=∠BAB′+∠CAB′,
即∠C′AB′=∠CAB,
在△C′AB′和△CAB中,AC′=AC,∠C′AB′=∠CAB,AB′=AB,
∴△C′AB′≌△CAB,
∴BC=B′C′.
分析:求出∠C′AC=∠B′AB=90°,推出∠C′AB′=∠CAB,根据SAS证出△C′AB′≌△CAB即可.
点评:本题考查了全等三角形的性质和判定的应用,关键是证出△C′AB′≌△CAB,题型较好,难度适中.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
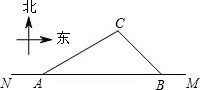 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上.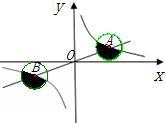 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为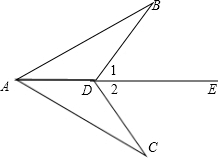 已知,如图,∠1=∠2,
已知,如图,∠1=∠2,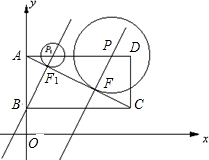 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为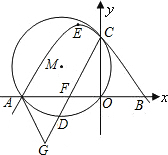 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧