Question

【题目】如图，等腰Rt△ABC（∠ACB=90°）的直角边与正方形DEFG的边长均为2，且AC与DE在同一直线上，开始时点C与点D重合，让△ABC沿这条直线向右平移，直到点A与点E重合为止．设CD的长为x，△ABC与正方形DEFG重合部分（阴影部分）的面积为y，

（1）求y与x之间的函数关系式；

（2）当△ABC与正方形DEFG重合部分的面积为时，求CD的长．

Answer 1

【答案】(1) y=x（2+2﹣x）=﹣x2+2x；y=（4﹣x）2；(2) CD=1或4﹣

【解析】试题分析：（1）按照x的取值范围分为当2≤x＜4时，当2≤x＜4时，分段根据重合部分的图形求面积；

（2）根据（1）的分段函数，分别令y=，列方程求x的值，再根据x的取值范围进行取舍．

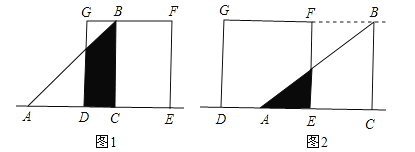
试题解析：解：（1）①如图1，当0＜x＜2时，y=x（2+2﹣x）=﹣x2+2x；

②如图2，当2≤x＜4时，y=（4﹣x）2；

（2）①当0＜x＜2时，﹣x2+2x=，解得x1=3，x2=1，∵0＜x＜2，∴x=1，②当2≤x＜4时， （4﹣x）2=，解得x1=4+，x2=4﹣，∵2≤x＜4，∴x=4﹣，∴CD=1或4﹣．