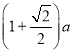题目内容
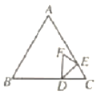
【题目】如图,等边![]() 中,AB=6,点D在BC上,BD=4,点E为边AC上一动点(不与点C重合),
中,AB=6,点D在BC上,BD=4,点E为边AC上一动点(不与点C重合),![]() 关于DE的轴对称图形为
关于DE的轴对称图形为![]() .
.
(1)当点F在AC上时,求证:DF//AB;
(2)设![]() 的面积为S1,
的面积为S1,![]() 的面积为S2,记S=S1-S2,S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;
的面积为S2,记S=S1-S2,S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;
(3)当B,F,E三点共线时。求AE的长。
【答案】(1)见解析;(2)![]() 存在最大值,
存在最大值,![]() 最大值为
最大值为![]() ;(3)
;(3)![]() .
.
【解析】
(1)由折叠的性质和等边三角形的性质可得∠DFC=∠A,可证DF∥AB;
(2)过点D作DM⊥AB交AB于点M,由题意可得点F在以D为圆心,DF为半径的圆上,由△ACD的面积为S1的值是定值,则当点F在DM上时,S△ABF最小时,S最大;
(3)过点D作DG⊥EF于点G,过点E作EH⊥CD于点H,由勾股定理可求BG的长,通过证明△BGD∽△BHE,可求EC的长,即可求AE的长.
解:(1)∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
由折叠可知:DF=DC,且点F在AC上,
∴∠DFC=∠C=60°,
∴∠DFC=∠A,
∴DF∥AB;
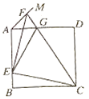
(2)存在,如图,
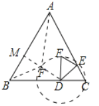
过点D作DM⊥AB交AB于点M,
∵AB=BC=6,BD=4,∴CD=2,∴DF=2,
∴点F在以D为圆心,DF为半径的圆上,
∴当点F在DM上时,S△ABF最小,
∵BD=4,DM⊥AB,∠ABC=60°,
∴MD=2![]() ,
,
∴S△ABF的最小值=![]() ,
,
∴S最大值=![]() .
.
(3)如图,过点![]() 作
作![]() 于点G,过点E作EH⊥CD于点H,
于点G,过点E作EH⊥CD于点H,
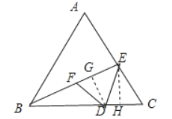
∵△CDE关于DE的轴对称图形为△FDE,
∴DF=DC=2,∠EFD=∠C=60°,
∵GD⊥EF,∠EFD=60°,
∴FG=1,DG=![]() FG=
FG=![]() ,
,
∵BD2=BG2+DG2,
∴16=3+(BF+1)2,
∴BF=![]() -1,
-1,
∴BG=![]() ,
,
∵EH⊥BC,∠C=60°,
∴CH=![]() ,EH=
,EH=![]() HC=
HC=![]() ,
,
∵∠GBD=∠EBH,∠BGD=∠BHE=90°,
∴△BGD∽△BHE,
∴![]() ,
,
∴ ,
,
∴EC=![]()
∴AE=AC-EC=![]()