Question

【题目】如图，Rt△ABC，∠ACB＝90°.分别以AB，AC为边作正方形ABEF和正方形ACMN，连接FN.若AC＝4，BC＝3，则S△ANF＝______.

Answer 1

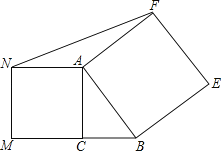
【答案】6

【解析】

过F作FH⊥NA交NA的延长线于H，根据正方形的性质和已知条件可证明△ACB≌△AHF，由此可得FH＝BC＝3，进而可求出S△ANF.

解：如图，过F作FH⊥AH交NA的延长线于H，

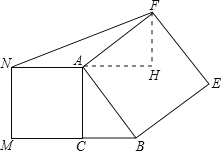
∵分别以AB，AC为边作正方形ABEF和正方形ACMN，

∴AB＝AF，∠ACB＝∠BAF＝90°，

∴∠CAB+∠BAH＝∠BAH+∠HAF＝90°，

∴∠CAB＝∠FAH，

在△ACB和△AHF中，

，

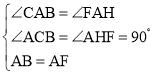∴△ACB≌△AHF，

∴BC＝HF＝3，

∵S△ANF＝×4×3＝6，

故答案为：6.