题目内容
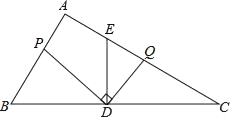
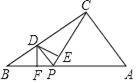
【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点P在边AB上,∠CPB的平分线交边BC于点D,DE⊥CP于点E,DF⊥AB于点F.当△PED与△BFD的面积相等时,BP的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据勾股定理得到AB=5,根据角平分线的性质得到DE=DF,根据全等三角形的性质得到BF=PF,根据相似三角形的性质即可得到结论.
解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5,
∵PD平分∠BPC,DF⊥PB,DE⊥PC,
∴DE=DF,
在Rt△PDF与Rt△PDE中,![]() ,
,
∴Rt△PDF≌Rt△PDE(HL),
∴S△PDF=S△PDE,
当△PED与△BFD的面积相等时,
∴S△PDF=S△BDF,
∴BF=PF,
∴BD=PD,
∴∠B=∠BPD=∠CPD,
∵∠BFD=∠ACB=90°,
∴△BDF∽△BAC,
∴![]() ,
,
∴![]() ,
,
∵∠PCD=∠BCP,
∴△BCP∽△PCD,
∴![]() ,
,
∴PC=![]() ,
,
∴CD=![]() ,
,
∴BD=![]() ,
,
∴PB=![]() .
.
故选:D.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目