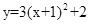题目内容
如图,已知二次函数y=ax2+bx+c的图象与y轴正半轴的交点在(0,2)的下方,与 轴的交点为(x1,0)和(2,0),且-2<x1<-1,则下列结论正确的是( )
轴的交点为(x1,0)和(2,0),且-2<x1<-1,则下列结论正确的是( )
A. | B. | C. | D. |
C.
解析试题分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
A、∵抛物线开口方向向下,∴a<0.
∵抛物线与x轴的交点是(2,0)和(x1,0),其中-2<x1<-1,
∴对称轴x=- >0,
>0,
∴b>0.
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0.故本选项错误;
B、根据图示知,当x=-1时,y>0,即a-b+c>0.故本选项错误;
C、∵把x=2代入y=ax2+bx+c得:y=4a+2b+c=0,
4a+2b=-c,
2a+b=- ,
,
∵O<c<2,
∴2a+b+1>0.
故本选项正确;
D、∵两个根之和为正,即 >1,即a<-b<0,
>1,即a<-b<0,
∴a+b<0.故本选项错误;
故选C.
考点: 二次函数图象与系数的关系.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
若二次函数 的图象经过点P(2,8),则该图象必经过点
的图象经过点P(2,8),则该图象必经过点
| A.(2,-8) | B.(-2,8) | C.(8,-2) | D.(-8,2) |
如图,已知二次函数y=x2+bx+c的图象如图所示,若y<0,则x的取值范围是 
| A.-1<x<4 | B.-1<x<3 |
| C.x<-1或x>4 | D.x<-1或x>3 |
已知抛物线 ,a是常数且
,a是常数且 ,下列选项中可能是它大致图像的是( )
,下列选项中可能是它大致图像的是( )
A. | B. | C. | D.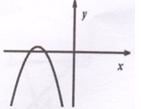 |
将函数y=2x2的图象向右平行移动1个单位,再向上平移5个单位,可得到的抛物线是( )
A. | B. |
C. | D. |
若二次函数 的图象经过点P(-3,2),则该图象必经过点( )
的图象经过点P(-3,2),则该图象必经过点( )
| A.(2,3) | B.(-2,-3) | C.(3,2) | D.(-3,-2) |
抛物线y=3(x-2)2+1图象上平移2个单位,再向左平移2个单位所得的解析式为 ( )
| A.y=3x2+3 | B.y=3x2-1 | C.y=3(x-4)2+3 | D.y=3(x-4)2-1 |
若双曲线 如下图所示,那么二次函数
如下图所示,那么二次函数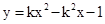 的图象大致为( )
的图象大致为( )
A. | B. | C.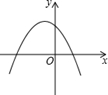 | D. |
 先向左平移1个单位,再向上平移2个单位,那么所得的新抛物线的解析式是( )
先向左平移1个单位,再向上平移2个单位,那么所得的新抛物线的解析式是( )