Question

已知半径分别为9和1的两圆相外切，那么它们的外公切线长为

 

．

Answer 1

分析：连接O₁O₂、O₁A、O₂B，过O₂向AO₁作平行于AB的直线交AO₁于C．在Rt△CO₁O₂中，利用勾股定理可求得CO₂的值即为AB的值．

解答：解：连接O₁O₂、O₁A、O₂B，过O₂向AO₁作平行于AB的直线交AO₁于C．
如图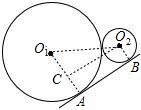：∵AB为圆O₁和圆O₂的外切线，
又CO₂∥AB，
∴△CO₁O₂为直角三角形；
∵AO₁=9，BO₂=1，
∴CO₁=9-1=8．
∴CO₂=

(O1O2)2-(CO1)2

=

102-82

=6．
故它们的外公切线长为6．

点评：考查圆的切线性质和勾股定理．