题目内容
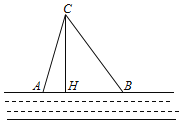
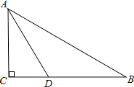
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() .
.
(1)求![]() ;
;
(2)求![]() .
.
【答案】(1)60°;(2)![]()
【解析】
(1)在直角三角形ABC中,由AD与AC的长,利用勾股定理求出CD的长,可得出CD为斜边AD的一半,利用直角三角形中一直角边等于斜边的一半,此直角边所对的角为30°,可得出∠CAD=30°,再由AD为角平分线得到一对角相等,都为30°,可得出∠CAB的度数,利用直角三角形的两锐角互余可得出∠B的度数;
(2)由(1)得出∠BAD=∠B,利用等角对等边得到AD=BD,由AD的长求出BD的长,再由CD+BD求出CB的长,直角三角形ABC的面积等于两直角边乘积的一半,求出即可.
(1)在Rt△ACD中,∠C=90°,AD=2![]() ,AC=3,根据勾股定理得:CD=
,AC=3,根据勾股定理得:CD=![]() =
=![]() ,∴CD=
,∴CD=![]() AD,∴∠CAD=30°.
AD,∴∠CAD=30°.
又∵AD为∠BAC的平分线,∴∠CAD=∠BAD=30°,即∠CAB=2∠CAD=60°,则∠B=90°﹣60°=30°;
(2)∵∠BAD=∠B=30°,∴AD=BD=2![]() .
.
又∵CD=![]() ,∴CB=CD+BD=3
,∴CB=CD+BD=3![]() ,则S△ABC=
,则S△ABC=![]() ACCB=
ACCB=![]() ×3×3
×3×3![]() =
=![]() .
.

练习册系列答案
相关题目
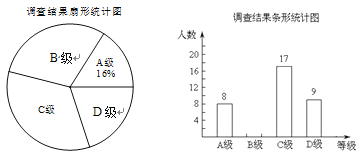
【题目】某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计解析,绘制了如下不完整的统计表和统计图(图).
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?