题目内容
 如图,已知△ABC,AC=BC=6,∠C=90度.O是AB的中点,⊙O与AC相切于点D、与BC相切于点E.设⊙O交OB于F,连DF并延长交CB的延长线于G.
如图,已知△ABC,AC=BC=6,∠C=90度.O是AB的中点,⊙O与AC相切于点D、与BC相切于点E.设⊙O交OB于F,连DF并延长交CB的延长线于G.(1)∠BFG与∠BGF是否相等?为什么?
(2)求由DG、GE和弧ED所围成图形的面积.(阴影部分)
分析:(1)连接OD.根据切线的性质得到OD⊥AC,则OD∥BC;可得∠ODF=∠G,再结合对顶角相等和等边对等角得到∠BFG=∠BGF.
(2)阴影部分的面积=直角三角形CDG的面积-(正方形的面积-扇形ODE的面积).根据等腰直角三角形的性质可求出有关边AB、OD的长,以及圆心角∠DOE的度数.进而可根据扇形的面积和直角三角形的面积求得阴影部分的面积.
(2)阴影部分的面积=直角三角形CDG的面积-(正方形的面积-扇形ODE的面积).根据等腰直角三角形的性质可求出有关边AB、OD的长,以及圆心角∠DOE的度数.进而可根据扇形的面积和直角三角形的面积求得阴影部分的面积.
解答: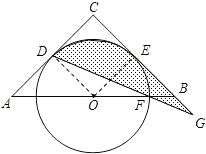 解:(1)∠BFG=∠BGF;理由如下:
解:(1)∠BFG=∠BGF;理由如下:
连OD,
∵OD=OF(⊙O的半径),
∴∠ODF=∠OFD;
∵⊙O与AC相切于点D,∴OD⊥AC;
又∵∠C=90°,即GC⊥AC,∴OD∥GC,
∴∠BGF=∠ODF;
又∵∠BFG=∠OFD,
∴∠BFG=∠BGF.
(2)连OE,
∵⊙O与AC相切于点D、与BC相切于点E,
∴DC=CE,OD⊥AC,OE⊥BC,
∵∠C=90°,
∴四边形ODCE为正方形,
∵AO=BO=
AB=
=3
,
∴OD=
BC=
×6=3,
∵∠BFG=∠BGF,
∴BG=BF=OB-OF=3
-3;
从而CG=CB+BG=3+3
;
∴S阴影=S△DCG-S正方形ODCE+S扇形ODE
=S△DCG-(S正方形ODCE-S扇形ODE)
=
•3•(3+3
)-(32-
π•32)
=
+
-
.
 解:(1)∠BFG=∠BGF;理由如下:
解:(1)∠BFG=∠BGF;理由如下:连OD,
∵OD=OF(⊙O的半径),
∴∠ODF=∠OFD;
∵⊙O与AC相切于点D,∴OD⊥AC;
又∵∠C=90°,即GC⊥AC,∴OD∥GC,
∴∠BGF=∠ODF;
又∵∠BFG=∠OFD,
∴∠BFG=∠BGF.
(2)连OE,
∵⊙O与AC相切于点D、与BC相切于点E,
∴DC=CE,OD⊥AC,OE⊥BC,
∵∠C=90°,
∴四边形ODCE为正方形,
∵AO=BO=
| 1 |
| 2 |
| 1 |
| 2 |
| AC2+BC2 |
| 2 |
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BFG=∠BGF,
∴BG=BF=OB-OF=3
| 2 |
从而CG=CB+BG=3+3
| 2 |
∴S阴影=S△DCG-S正方形ODCE+S扇形ODE
=S△DCG-(S正方形ODCE-S扇形ODE)
=
| 1 |
| 2 |
| 2 |
| 1 |
| 4 |
=
| 9π |
| 4 |
9
| ||
| 2 |
| 9 |
| 2 |
点评:此题综合考查了切线的性质、平行线的性质、等腰直角三角形的性质及扇形的面积计算方法.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.
24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH. 如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.
如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°. 17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
 20、如图,已知△ABC是锐角三角形,且∠A=50°,高BE、CF相交于点O,求∠BOC的度数.
20、如图,已知△ABC是锐角三角形,且∠A=50°,高BE、CF相交于点O,求∠BOC的度数.