题目内容
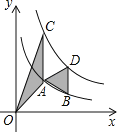
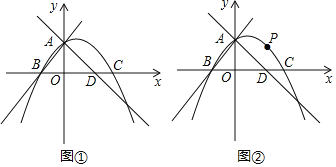
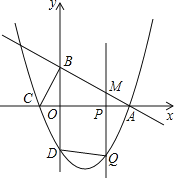
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴,y轴于点A,B抛物线
分别交x轴,y轴于点A,B抛物线![]() 经过点A,且交x轴于另外一点C,交y轴于点D.
经过点A,且交x轴于另外一点C,交y轴于点D.
(1)求抛物线的表达式;
(2)求证:AB⊥BC;
(3)点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m,当以B,D,Q,M为顶点的四边形是平行四边形时,求m的值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)见解析;(3)m的值是2或1+
x﹣2;(2)见解析;(3)m的值是2或1+![]() 或1﹣
或1﹣![]() .
.
【解析】
(1)令y=﹣![]() x+2=0,解得:x=4,即可求解,然后把点A的坐标代入抛物线解析式,借助于方程求得a的值即可;
x+2=0,解得:x=4,即可求解,然后把点A的坐标代入抛物线解析式,借助于方程求得a的值即可;
(2)把由函数图象上点的坐标特征求得点B、C的坐标,然后利用两点间的距离公式和勾股定理的逆定理证得结论;
(3)以B、D、Q,M为顶点的四边形是平行四边形时,利用|MQ|=BD即可求解.
(1)令y=﹣![]() x+2=0,解得:x=4,y=0,则x=2,
x+2=0,解得:x=4,y=0,则x=2,
即:点A坐标为:(4,0).
代入![]() 中,得16a﹣8=0,得a=
中,得16a﹣8=0,得a=![]() .
.
∴该抛物线解析式为:y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
(2)由(1)知,抛物线解析式为:y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
∴当y=0时,x1=﹣1,x2=4,的C(﹣1,0).
故OC=1.
于是AB2=20,BC2=5,AC2=25.
从而AB2+BC2=AC2.
∴AB⊥BC;
(3)由(1)知,抛物线解析式为: ![]() .
.
当x=0时,y=2,得D(0,﹣2),
∴BD=4.
当MQ=(﹣![]() m+2)﹣
m+2)﹣![]() =
=![]() ﹣m﹣4=4时,得m=2或m=0(舍去).
﹣m﹣4=4时,得m=2或m=0(舍去).
当MQ=(![]() m2﹣
m2﹣![]() m﹣2)﹣(﹣
m﹣2)﹣(﹣![]() m+2)=
m+2)=![]() ﹣m﹣4=4时,得m=1+
﹣m﹣4=4时,得m=1+![]() 或m=1﹣
或m=1﹣![]() .
.
综上所述,m的值是2或1+![]() 或1﹣
或1﹣![]() .
.

练习册系列答案
相关题目