题目内容
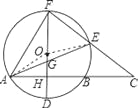
【题目】如图,⊙O的直径FD⊥弦AB于点H,E是![]() 上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.
上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.

(1)求⊙O的直径FD;
(2)在E点运动的过程中,EFCF的值是否为定值?若是,求出其定值;若不是,请说明理由;
(3)当E点运动到![]() 的中点时,连接AE交DF于点G,求△FEA的面积.
的中点时,连接AE交DF于点G,求△FEA的面积.
【答案】(1)DF=10;(2)是,EFCF=80;(3)S△FEA=30.
【解析】分析:(1)连接OA,由垂径定理得到AH=![]() AB=4,设OA=x,在Rt△OAH中,根据勾股定理列方程即可得到结论;(2)根据垂径定理得到
AB=4,设OA=x,在Rt△OAH中,根据勾股定理列方程即可得到结论;(2)根据垂径定理得到![]() ,根据圆周角定理得到∠BAF=∠AEF,推出△FAE∽△FCA,根据相似三角形的性质得到
,根据圆周角定理得到∠BAF=∠AEF,推出△FAE∽△FCA,根据相似三角形的性质得到![]() ,推出AF=EFCF,代入数据即可得到结论;(3)连接OE,由E点是
,推出AF=EFCF,代入数据即可得到结论;(3)连接OE,由E点是![]() 的中点,得到∠FAE=45°,∠EOF=90°,于是得到∠EOH=∠AHG,推出△OGE∽△HGA,根据相似三角形的性质得到
的中点,得到∠FAE=45°,∠EOF=90°,于是得到∠EOH=∠AHG,推出△OGE∽△HGA,根据相似三角形的性质得到![]() ,求得OG=
,求得OG=![]() ,得到FG=OF+OG=
,得到FG=OF+OG=![]() ,根据三角形的面积公式即可得到结论.
,根据三角形的面积公式即可得到结论.
本题解析:(1)连接OA,∵直径FD⊥弦AB于点H,∴AH=![]() AB=4,设OA=x,
AB=4,设OA=x,
在Rt△OAH中,AO2=AH2+![]() ,即x2=42+
,即x2=42+![]() ,∴x=5,
,∴x=5,
∴DF=2OA=10;
(2)是,
∵直径FD⊥弦AB于点H,∴![]() ,∴∠BAF=∠AEF,
,∴∠BAF=∠AEF,
∵∠AFE=∠CFA,∴△FAE∽△FCA,∴![]() ,∴AF2=EFCF,
,∴AF2=EFCF,
在Rt△AFH中,AF2=AH2+FH2=44+82=80,
∴EFCF=80;
(3)连接OE,∵E点是![]() 的中点,∴∠FAE=45°,∠EOF=90°,
的中点,∴∠FAE=45°,∠EOF=90°,
∴∠EOH=∠AHG,∵∠OGE=∠HGA,∴△OGE∽△HGA,
∴![]() ,即
,即![]()
![]() =
=![]() ,∴OG=
,∴OG=![]() ,∴FG=OF+OG=
,∴FG=OF+OG=![]() ,
,
∴S△FEA=S△EFG+S△AFG=![]() FGOE+
FGOE+![]() FGAH=
FGAH=![]() ×
×![]() ×(4+5)=30.
×(4+5)=30.