ЬтФПФкШн
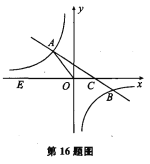
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЌBЕФзјБъЗжБ№ЮЊA(aЃЌ0)ЃЌB(bЃЌ0)ЃЌЧвaЃЌbТњзу|2a+6|+(2aЉ3b+12)2ЃН0ЃЌЯжЭЌЪБНЋЕуAЃЌBЗжБ№ЯђзѓЦНвЦ2ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ2ИіЕЅЮЛЃЌЗжБ№ЕУЕНЕуAЃЌBЕФЖдгІЕуCЃЌDЃЌСЌНгACЃЌBDЃЎ
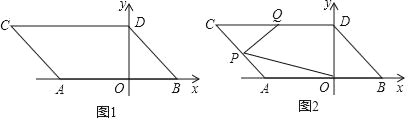
(1)ЧыжБНгаДГіAЁЂBЁЂCЁЂDЫФЕуЕФзјБъЃЛ
(2)ШчЭМ2ЃЌЕуPЪЧЯпЖЮACЩЯЕФвЛИіЖЏЕуЃЌЕуQЪЧЯпЖЮCDЕФжаЕуЃЌСЌНгPQЃЌPOЃЌЕБЕуPдкЯпЖЮACЩЯвЦЖЏЪБ(ВЛгыAЃЌCжиКЯ)ЃЌЧыевГіЁЯPQDЃЌЁЯOPQЃЌЁЯPOBЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
(3)дкзјБъжсЩЯЪЧЗёДцдкЕуMЃЌЪЙШ§НЧаЮMADЕФУцЛ§гыШ§НЧаЮACDЕФУцЛ§ЯрЕШЃПШєДцдкЃЌжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЪдЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉA(Љ3ЃЌ0)ЃЌB(2ЃЌ0)ЃЌCЃЈ-5ЃЌ2ЃЉЃЌDЃЈ0ЃЌ2ЃЉЃЛЃЈ2ЃЉЁЯPQD+ЁЯOPQ+ЁЯPOBЃН360ЁуЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ(2ЃЌ0)Лђ(Љ8ЃЌ0)Лђ(0ЃЌЉ![]() )Лђ(0ЃЌ
)Лђ(0ЃЌ![]() )
)
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнОјЖджЕЕФЗЧИКадЁЂХМДЮЗНЕФЗЧИКадЗжБ№ЧѓГіaЁЂbЃЌЕУЕНЕуAЃЌBЕФзјБъЃЌМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЧѓГіЮхБпаЮQPOBDЕФФкНЧКЭЃЌИљОнЦНааЯпЕФаджЪЕУЕНЁЯQDBЃЋЁЯOBDЃН180ЁуЃЌМЦЫуМДПЩЃЛ
ЃЈ3ЃЉИљОнЬтвтЧѓГіЁїACDЕФУцЛ§ЃЌЗжЕуMдкxжсЩЯЁЂЕуMдкyжсЩЯСНжжЧщПіЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМЦЫуМДПЩЃЎ
НтЃК(1)Ёп|2a+6|+(2aЉ3b+12)2ЃН0ЃЌ
Ёр|2a+6|ЃН0ЃЌ(2aЉ3b+12)2ЃН0ЃЌ
НтЕУЃЌaЃНЉ3ЃЌbЃН2ЃЌ
дђЕуAЃЌBЕФзјБъЗжБ№ЮЊA(Љ3ЃЌ0)ЃЌB(2ЃЌ0)ЃЛ
НЋЕуAЃЌBЗжБ№ЯђзѓЦНвЦ2ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ2ИіЕЅЮЛЃЌЗжБ№ЕУЕНЕуAЃЌBЕФЖдгІЕуCЃЌDЃЌдђCЃЈ-5,2ЃЉDЃЈ0,2ЃЉЃЛ
(2)ЁЯPQD+ЁЯOPQ+ЁЯPOBЃН360ЁуЃЌ
РэгЩШчЯТЃКЮхБпаЮQPOBDЕФФкНЧКЭЃН(5Љ2)ЁС180ЁуЃН540ЁуЃЌ
ЁпCDЁЮABЃЌ
ЁрЁЯQDB+ЁЯOBDЃН180ЁуЃЌ
ЁрЁЯPQD+ЁЯOPQ+ЁЯPOBЃН540ЁуЉ(ЁЯQDB+ЁЯOBD)ЃН360ЁуЃЛ
(3)гЩЬтвтЕУЃЌЕуCЕФзјБъЮЊ(Љ5ЃЌ2)ЃЌЕуDЕФзјБъЮЊ(0ЃЌ2)ЃЌ
дђЁїACDЕФУцЛ§ЃН![]() ЁС5ЁС2ЃН5ЃЌ
ЁС5ЁС2ЃН5ЃЌ
ЕБЕуMдкxжсЩЯЪБЃЌЩшЕуMЕФзјБъЮЊ(xЃЌ0)ЃЌ
дђAMЃН|Љ3Љx|ЃЌ
гЩЬтвтЕУЃЌ![]() ЁС|Љ3Љx|ЁС2ЃН5ЃЌ
ЁС|Љ3Љx|ЁС2ЃН5ЃЌ
НтЕУЃЌxЃН2ЛђЉ8ЃЌ
ЕБЕуMдкyжсЩЯЪБЃЌЩшЕуMЕФзјБъЮЊ(0ЃЌy)ЃЌ
дђAMЃН|2Љy|ЃЌ
гЩЬтвтЕУЃЌ![]() ЁС|2Љy|ЁС3ЃН5ЃЌ
ЁС|2Љy|ЁС3ЃН5ЃЌ
НтЕУЃЌyЃНЉ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌШ§НЧаЮMADЕФУцЛ§гыШ§НЧаЮACDЕФУцЛ§ЯрЕШЪБЃЌЕуMЕФзјБъЮЊ(2ЃЌ0)Лђ(Љ8ЃЌ0)Лђ(0ЃЌЉ![]() )Лђ(0ЃЌ
)Лђ(0ЃЌ![]() )ЃЎ
)ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПЮваЃОйааЁАККзжЬ§аДЁББШШќЃЌУПЮЛбЇЩњЬ§аДККзж39ИіЃЌБШШќНсЪјКѓЫцЛњГщВщВПЗжбЇЩњЕФЬ§аДНсЙћЃЌвдЯТЪЧИљОнГщВщНсЙћЛцжЦЕФЭГМЦЭМЕФвЛВПЗжЃЎ
зщБ№ | е§ШЗЪ§зжx | ШЫЪ§ |
A | 0ЁмxЃМ8 | 10 |
B | 8ЁмxЃМ16 | 15 |
C | 16ЁмxЃМ24 | 25 |
D | 24ЁмxЃМ32 | m |
E | 32ЁмxЃМ40 | n |
ИљОнвдЩЯаХЯЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкЭГМЦБэжаЃЌm=ЁЁ ЁЁЃЌn=ЁЁ ЁЁЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЁАCзщЁБЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЪЧЁЁ ЁЁЃЎ
ЃЈ3ЃЉгаШ§ЮЛЦРЮЏРЯЪІЃЌУПЮЛРЯЪІдкEзщбЇЩњЭъГЩбЇаЃБШШќКѓЃЌГіЪОЁАЭЈЙ§ЁБЛђЁАЬдЬЁБЛђЁАД§ЖЈЁБЕФЦРЖЈНсЙћЃЎбЇаЃЙцЖЈЃКУПЮЛбЇЩњжСЩйЛёЕУСНЮЛЦРЮЏРЯЪІЕФЁАЭЈЙ§ЁБВХФмДњБэбЇаЃВЮМгЖѕжнЪаЁАККзжЬ§аДЁББШШќЃЌЧыгУЪїаЮЭМЧѓГіEзщбЇЩњЭѕдЦВЮМгЖѕжнЪаЁАККзжЬ§аДЁББШШќЕФИХТЪЃЎ