题目内容
（1998•四川）一船在A处观测到西北方向有一座灯塔B，这只船沿正西方向以每小时25海里的速度航行1小时12分钟后到达C处，这时测得灯塔B在北偏东26°方向．求灯塔B到C处的距离（结果用含锐角三角函数的式子表示）．分析：过B点作BD⊥CA于D．根据路程=速度×时间可求AC的长，设BD=x，根据三角函数可得CD的长，再根据AC=CD+DA=30可得关于x的方程，解方程求得x的值，再根据三角函数的知识得到BC的长．
解答：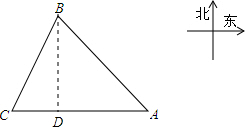
解：过B点作BD⊥CA于D．
AC=25×1.2=30（海里），
设BD=x，则CD=xctg（90°-26°）=xcot64°，
AC=CD+DA=xcot64°+x=30，
解得x=
．
在Rt△BCD中，BC=
，
则BC=
=
．
解：过B点作BD⊥CA于D．AC=25×1.2=30（海里），
设BD=x，则CD=xctg（90°-26°）=xcot64°，
AC=CD+DA=xcot64°+x=30，
解得x=
| 30 |
| 1+cot64° |
在Rt△BCD中，BC=
| x |
| sin64° |
则BC=
| 30 |
| sin64°(1+cot64°) |
| 30 |
| sin64°+cot64° |
点评：考查了解直角三角形的应用-方向角问题，解一般三角形的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
练习册系列答案
相关题目