题目内容
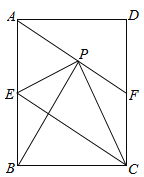
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.
【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】
试题分析:(1)由折叠的性质得到BE=PE,EC⊥PB,根据E为AB中点,得到AE=PE,利用等角对等边得到两对角相等,利用外角性质得到∠AEP=2∠EPB,设∠EPB=x,则∠AEP=2x,表示出∠APE,由∠APE+∠EPB得到∠APB为90°,进而得到AF与EC平行,再由AE与FC平行,利用两对边平行的四边形为平行四边形即可得证;
(2)根据等边三角形性质,得到△AEP三条边相等,三内角相等,再由折叠的性质及邻补角定义得到一对角相等,根据同角的余角相等得到一对角相等,再由AP=EB,利用AAS即可得证;
(3)过P作PM⊥CD,在Rt△EBC中,利用勾股定理求出EC,利用面积求出BQ,再根据BP=2BQ求出BP,在Rt△ABP中,利用勾股定理求出AP,根据AF-AP求出PF,由PM与AD平行,得到△PMF与△ADF相似,由相似得比例求出PM,再由FC=AE=3,求出△CPF面积即可.
试题解析:(1)由折叠得到BE=PE,EC⊥PB,∵E为AB的中点,∴AE=EB,即AE=PE,∴∠EBP=∠EPB,∠EAP=∠EPA,∵∠AEP为△EBP的外角,∴∠AEP=2∠EPB,设∠EPB=x,则∠AEP=2x,∠APE=![]() =90°﹣x,∴∠APB=∠APE+∠EPB=x+90°﹣x=90°,即BP⊥AF,∴AF∥EC,∵AE∥FC,∴四边形AECF为平行四边形;
=90°﹣x,∴∠APB=∠APE+∠EPB=x+90°﹣x=90°,即BP⊥AF,∴AF∥EC,∵AE∥FC,∴四边形AECF为平行四边形;
(2)∵△AEP为等边三角形,∴∠BAP=∠AEP=60°,AP=AE=EP=EB,∵∠PEC=∠BEC,∴∠PEC=∠BEC=60°,∵∠BAP+∠ABP=90°,∠ABP+∠BEQ=90°,∴∠BAP=∠BEQ,在△ABP和△EBC中,∵∠APB=∠EBC=90°,∠BAP=∠BEQ,AP=EB,∴△ABP≌△EBC(AAS),∵△EBC≌△EPC,∴△ABP≌△EPC;
(3)过P作PM⊥DC,交DC于点M,在Rt△EBC中,EB=3,BC=4,根据勾股定理得:EC=![]() =5,∵S△EBC=
=5,∵S△EBC=![]() EBBC=
EBBC=![]() ECBQ,∴BQ=
ECBQ,∴BQ=![]() =
=![]() ,由折叠得:BP=2BQ=
,由折叠得:BP=2BQ=![]() ,在Rt△ABP中,AB=6,BP=
,在Rt△ABP中,AB=6,BP=![]() ,根据勾股定理得:AP=
,根据勾股定理得:AP=![]() =
=![]() ,∵四边形AECF为平行四边形,∴AF=EC=5,FC=AE=3,∴PF=
,∵四边形AECF为平行四边形,∴AF=EC=5,FC=AE=3,∴PF=![]() =
=![]() ,∵PM∥AD,∴
,∵PM∥AD,∴![]() ,即
,即 ,解得:PM=
,解得:PM=![]() ,则S△PFC=
,则S△PFC=![]() FCPM=
FCPM=![]() =
=![]() .
.