题目内容
如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC= .设直线AC
.设直线AC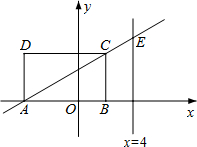 与直线x=4交于点E.
与直线x=4交于点E.
(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.
解:(1)设抛物线的函数关系式为:y=a(x-4)2+m,
∵抛物线过C与原点O,
∴ ,
,
解得: ,
,
∴所求抛物线的函数关系式为:y=- (x-4)2+
(x-4)2+ ,
,
设直线AC的函数关系式为y=kx+b,
 ,
,
解得: .
.
∴直线AC的函数关系式为:y= x+
x+ ,
,
∴点E的坐标为(4, )
)
∴此抛物线过E点.
(2)过M作MQ∥y轴,交x轴于Q,交直线CN于P;
易知:N(8,0),C(2,2 );
);
可得直线CN的解析式为y=- x+
x+ ;
;
设点Q的坐标为(m,0),则P(m,- m+
m+ ),M(m,-
),M(m,- m2+
m2+ m);
m);
∴MP=- m2+
m2+ m-(-
m-(- m+
m+ )=-
)=- m2+
m2+ m-
m- ;
;
∴S=S△CMN=S△CPM+S△MNP= MP•|xM-xC|+
MP•|xM-xC|+ MP•|xN-xM|=
MP•|xN-xM|= MP•|xN-xC|=
MP•|xN-xC|= ×(-
×(- m2+
m2+ m-
m- )×6=-
)×6=- m2+5
m2+5 m-8
m-8 ;
;
即S=- (m-5)2+
(m-5)2+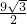 (2<m<8);
(2<m<8);
∵2<5<8,
∴当m=5时,Smax=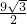 ;
;
即△CMN的最大面积为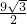 .
.
分析:(1)设直线x=4与x轴的交点为F,易证得△ABC∽△AFE,根据相似三角形得到的比例线段即可求出EF的长,也就得到了E点的坐标;可用待定系数法求出抛物线的解析式,然后将E点坐标代入其中进行判断即可;
(2)过M作y轴的平行线,交直线CN于P,交x轴于Q;根据抛物线的解析式可求出N点的坐标,进而可求出直线CN的解析式,设出Q点的坐标,即可根据抛物线和直线的解析式求出MP的长;以MP为底,C、N的横坐标差的绝对值为高即可得到△CMN的面积,由此可求出关于△CMN的面积与Q点横坐标的函数关系式,根据函数的性质即可得到△CMN的最大面积.
点评:本题着重考查了待定系数法求二次函数解析式、函数图象交点坐标及图形面积的求法等重要知识点,综合性强,能力要求较高.考查学生数形结合的数学思想方法.
∵抛物线过C与原点O,
∴
 ,
,解得:
 ,
,∴所求抛物线的函数关系式为:y=-
 (x-4)2+
(x-4)2+ ,
,设直线AC的函数关系式为y=kx+b,
 ,
,解得:
 .
.
∴直线AC的函数关系式为:y=
 x+
x+ ,
,∴点E的坐标为(4,
 )
) ∴此抛物线过E点.
(2)过M作MQ∥y轴,交x轴于Q,交直线CN于P;
易知:N(8,0),C(2,2
 );
);可得直线CN的解析式为y=-
 x+
x+ ;
;设点Q的坐标为(m,0),则P(m,-
 m+
m+ ),M(m,-
),M(m,- m2+
m2+ m);
m);∴MP=-
 m2+
m2+ m-(-
m-(- m+
m+ )=-
)=- m2+
m2+ m-
m- ;
;∴S=S△CMN=S△CPM+S△MNP=
 MP•|xM-xC|+
MP•|xM-xC|+ MP•|xN-xM|=
MP•|xN-xM|= MP•|xN-xC|=
MP•|xN-xC|= ×(-
×(- m2+
m2+ m-
m- )×6=-
)×6=- m2+5
m2+5 m-8
m-8 ;
;即S=-
 (m-5)2+
(m-5)2+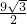 (2<m<8);
(2<m<8);∵2<5<8,
∴当m=5时,Smax=
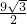 ;
;即△CMN的最大面积为
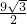 .
.分析:(1)设直线x=4与x轴的交点为F,易证得△ABC∽△AFE,根据相似三角形得到的比例线段即可求出EF的长,也就得到了E点的坐标;可用待定系数法求出抛物线的解析式,然后将E点坐标代入其中进行判断即可;
(2)过M作y轴的平行线,交直线CN于P,交x轴于Q;根据抛物线的解析式可求出N点的坐标,进而可求出直线CN的解析式,设出Q点的坐标,即可根据抛物线和直线的解析式求出MP的长;以MP为底,C、N的横坐标差的绝对值为高即可得到△CMN的面积,由此可求出关于△CMN的面积与Q点横坐标的函数关系式,根据函数的性质即可得到△CMN的最大面积.
点评:本题着重考查了待定系数法求二次函数解析式、函数图象交点坐标及图形面积的求法等重要知识点,综合性强,能力要求较高.考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
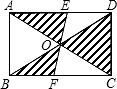 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为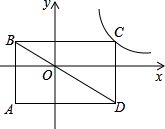 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y= 如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线
如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线 (2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( )
(2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( ) 如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=
如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=