题目内容
【题目】在△ABC中，AB=AC，点D是BC的中点，点E是AD上任意一点．
（1）如图1，连接BE、CE，问：BE=CE成立吗？并说明理由；
（2）如图2，若∠BAC=45°，BE的延长线与AC垂直相交于点F时，问：EF=CF成立吗？并说明理由．
【答案】（1）成立．（2）成立．见解析
【解析】
试题分析：（1）成立，根据等腰三角形的性质就可以求出∠BAE=∠CAE，再证明△ABE≌△ACE就可以得出结论；
（2）成立，由BF⊥AC，∠BAC=45°就可以求出AF=BF，在由条件证明△AEF≌△BCF就可以得出结论．
解：（1）成立．
理由：
∵AB=AC，D是BC的中点，∴∠BAE=∠CAE．
在△ABE和△ACE中，
∴△ABE≌△ACE（ SAS ）
∴BE=CE．
（2）成立．
理由：
∵∠BAC=45°，BF⊥AF．
∴△ABF为等腰直角三角形
∴AF=BF…
由（1）知AD⊥BC，
∴∠EAF=∠CBF
在△AEF和△BCF中，
．
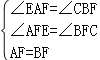∴△AEF≌△BCF（ AAS ），
∴EF=CF．
练习册系列答案
相关题目
【题目】某公司销售一种进价为20 （元/个）的计算器，其销售量y （万个）与销售价格x （元/个）之间为一次函数关系，其变化如下表：
价格x （元/个） | … | 30 | 50 | … |
销售量y （万个） | … | 5 | 3 | … |
同时，销售过程中的其他开支（不含进价）总计40万元．若该公司要获得40万元的净利润，且尽可能让顾客得到实惠，那么销售价格应定为多少？
（注：净利润=总销售额﹣总进价﹣其他开支）
