题目内容
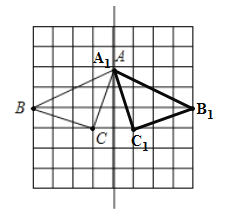
【题目】如图，在8×8的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）.
（1）在图中作出△ABC关于直线l对称的△A1B1C1；（要求：A与A1，B与B1，C与C1相对应）
（2）
是 三角形；
（3）若有一格点P到点A、B的距离相等（PA=PB），则网格中满足条件的点P共有 个；
(4)在直线
上找一点Q，使QB+QC的值最小。
【答案】（1）答案见解析；（2）等腰直角；（3）4；（4）答案见解析.
【解析】
（1）分别作出点A、B、C关于直线l的对称点，再顺次连接可得；
（2）根据网格，求出AB，AC，BC的长度，然后再判断即可；
（3）作线段AB的垂直平分线，即可得到答案；
（4）连接
，与
相交于一点，这点为点Q，由垂直平分线性质，QC=
，则得到QB+QC的最小值.
解：（1）如图所示：△A1B1C1为所求.
（2）根据题意，可知，
，
，
，
∴
，
∵
，
∴
是等腰直角三角形；
故答案为：等腰直角.
（3）如图，作线段AB的垂直平分线，与网格的顶点相交即为点P；
由图可知，使PA=PB的点P一共有4个，
故答案为：4.
（4）如图，连接与相交于点Q，则QB+QC取到最小值；
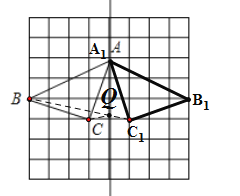
∵垂直平分
，
∴
，
∴QB+QC=QB+
，
∴最小值为：
；
练习册系列答案
相关题目
