题目内容
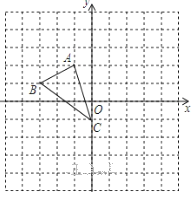
【题目】如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:
①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,在图中标出该圆弧所在圆的圆心D.
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:D( );
②⊙D的半径= (结果保留根号);
③利用网格试在图中找出格点E ,使得直线EC与⊙D相切(写出所有可能的结果).
【答案】(1)见解析;(2)①(2,0);②2![]() ;③(7,0).
;③(7,0).
【解析】
(1)根据题意建立平面直角坐标系,然后作出弦AB的垂直平分线,以及BC的垂直平分线,两直线的交点即为圆心D,连接AD,CD;
(2)①根据第一问画出的图形即可得出D的坐标;
②在直角三角形AOD中,由OA及OD的长,利用勾股定理求出AD的长,即为圆D的半径;
③根据半径相等得出CD=AD=2![]() ,设EF=x,在Rt△CDE和Rt△CEF中,根据勾股定理列出两个式子即可求出x的值,从而求出E点坐标
,设EF=x,在Rt△CDE和Rt△CEF中,根据勾股定理列出两个式子即可求出x的值,从而求出E点坐标
(1)根据题意画出相应的图形,如图所示:
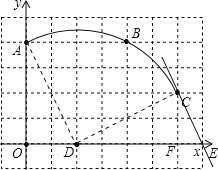
(2)①根据图形得:D(2,0);
②在Rt△AOD中,OA=4,OD=2,
根据勾股定理得:AD=![]() =2
=2![]()
则D的半径为2![]()
③∵EC与⊙D相切
∴CE⊥DC
∴△CDE为直角三角形即∠DCE=90°
∵AD和CD都是圆D的半径,
∴由②知,CD=AD=2![]()
设EF=x
在Rt△CDE中,(2![]() )2+CE2=(4+x)2
)2+CE2=(4+x)2
在Rt△CEF中,22+x2=CE2
∴(2![]() )2+(22+x2)=(4+x)2
)2+(22+x2)=(4+x)2
解得,x=1,即EF=1
∴OE=2+4+1=7
∴E点坐标为(7,0)

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目