题目内容
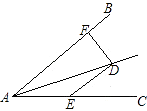
【题目】如图，已知，l1∥l2 ， C1在l1上，并且C1A⊥l2 ， A为垂足，C2 ， C3是l1上任意两点，点B在l2上．设△ABC1的面积为S1 ， △ABC2的面积为S2 ， △ABC3的面积为S3 ， 小颖认为S1=S2=S3 ， 请帮小颖说明理由
【答案】【解答】解：∵直线l1∥l2 ，
∴△ABC1 ， △ABC2 ， △ABC3的底边AB上的高相等，
∴△ABC1 ， △ABC2 ， △ABC3这3个三角形同底，等高，
∴△ABC1 ， △ABC2 ， △ABC3这些三角形的面积相等．
即S1=S2=S3 ．
【解析】根据两平行线间的距离相等，即可解答．
【考点精析】利用平行线之间的距离和三角形的面积对题目进行判断即可得到答案，需要熟知两条平行线的距离：两条直线平行，从一条直线上的任意一点向另一条直线引垂线，垂线段的长度，叫做两条平行线的距离；三角形的面积=1/2×底×高．
练习册系列答案
名校课堂系列答案
相关题目
