题目内容
一个一次函数的图象与直线y=
x-1平行,与x轴、y轴的交点分别为A,B,并且过点(-1,-5),则在线段AB上(包括端点A,B)横、纵坐标都是整数的点有( )
| 1 |
| 2 |
| A、4个 | B、5个 | C、6个 | D、7个 |
分析:首先根据一次函数的图象与直线y=
x-1平行,图象经过点(-1,-5),用待定系数法求出函数关系式,然后求出A,B两点的坐标,最后根据所求点满足在线段AB上(包括端点A,B),且横、纵坐标都是整数,得出结果.
| 1 |
| 2 |
解答:解:∵一次函数的图象与直线y=
x-1平行,设此直线为y=
x+b,
∵过点(-1,-5),
∴把此点代入,得-5=-
+b,
解得b=-
,
∴此直线为y=
x-
.
当x=0时,y=-
;y=0时,x=9.
故A(9,0),B(0,-
).
由直线的解析式可知,只要x是奇数时,y即为整数,
而从-10到0共有5个奇数,即-1,-3,-5,-7,-9,
故在线段AB上(包括端点A,B)横、纵坐标都是整数的点有5个.
故选B.
| 1 |
| 2 |
| 1 |
| 2 |
∵过点(-1,-5),
∴把此点代入,得-5=-
| 1 |
| 2 |
解得b=-
| 9 |
| 2 |
∴此直线为y=
| 1 |
| 2 |
| 9 |
| 2 |
当x=0时,y=-
| 9 |
| 2 |
故A(9,0),B(0,-
| 9 |
| 2 |
由直线的解析式可知,只要x是奇数时,y即为整数,
而从-10到0共有5个奇数,即-1,-3,-5,-7,-9,
故在线段AB上(包括端点A,B)横、纵坐标都是整数的点有5个.
故选B.
点评:本题要注意利用一次函数平行的特点,列出方程,求出未知数.再根据题意求解.

练习册系列答案
相关题目
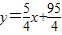 的图象与直线平行,与x轴、y轴的交点分别为A、B,并且过点(-1,-25),则在线段AB上(包括端点A、B),横、纵坐标都是整数的点有( )
的图象与直线平行,与x轴、y轴的交点分别为A、B,并且过点(-1,-25),则在线段AB上(包括端点A、B),横、纵坐标都是整数的点有( )