题目内容
已知⊙O内有一点M，过点M作圆的弦，在所有的弦中，最长的弦的长度为10cm，最短的弦的长度为8cm，则点M与圆心O的距离为分析：最长的弦的长度为10cm即圆的直径长是10cm，最短的弦的长度为8cm即过点M与直径OM垂直的弦长是8cm，利用垂径定理即可求解．
解答：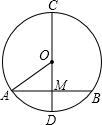
解：∵直径CD⊥弦AB
∴AM=
AB=
×8=4cm．
在直角△OAM中，OM=
=
=3cm．
故答案是：3cm．
解：∵直径CD⊥弦AB∴AM=
| 1 |
| 2 |
| 1 |
| 2 |
在直角△OAM中，OM=
| OA2-AM2 |
| 52-42 |
故答案是：3cm．
点评：本题是垂径定理的应用，正确理解经过圆中一点的弦中最长的弦与最短的弦的位置是解决本题的关键．
练习册系列答案
相关题目
已知平面内有一点P，它的横坐标与纵坐标互为相反数，且与原点的距离是2，则P点的坐标为（ ）
| A、（-1，1）或（1，-1） | ||||||||
| B、（1，-1） | ||||||||
C、（-
| ||||||||
D、（
|
如图，已知∠AOB内有一点P，过点P画MN∥OB交OA于C，过点P画PD⊥OA，垂足为D，并量出点P到OA距离．