题目内容
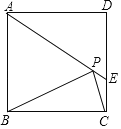
【题目】如图![]() ,一架
,一架![]() 米长的梯子
米长的梯子![]() 斜靠在与地面
斜靠在与地面![]() 垂直的墙
垂直的墙![]() 上,梯子
上,梯子![]() 与地面
与地面![]() 的倾斜角
的倾斜角![]() 为
为![]() .
.
![]() 求
求![]() 与
与![]() 的长;
的长;
![]() 若梯子顶端
若梯子顶端![]() 沿
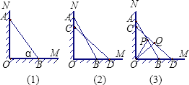
沿![]() 下滑,如图
下滑,如图![]() ,设
,设![]() 点下滑至
点下滑至![]() 点,
点,![]() 点向右滑行至
点向右滑行至![]() 点.若
点.若![]() ,试求梯子顶端
,试求梯子顶端![]() 沿
沿![]() 下滑多少米;
下滑多少米;
![]() 若梯子顶端
若梯子顶端![]() 沿
沿![]() 下滑,如图
下滑,如图![]() ,设
,设![]() 点下滑至
点下滑至![]() 点,
点,![]() 点向右滑行至
点向右滑行至![]() 点,梯子
点,梯子![]() 的中点
的中点![]() ,也随之运动到点
,也随之运动到点![]() ,若
,若![]() ,试求
,试求![]() 的长.
的长.

【答案】(1)![]() 米
米![]() 米;(2)梯子的顶端沿
米;(2)梯子的顶端沿![]() 下滑
下滑![]() 米;(3)
米;(3)![]() (米).
(米).
【解析】
(1)在直角△AOB中,已知斜边AB,和锐角∠ABO,即可根据正弦和余弦的定义求得OA,OB的长;
(2)利用AC:BD=2:3,设AC=2x(米)BD=3x(米)CD=4米,利用勾股定理列出关系式即可求得下滑的长度;
(3)根据P、Q分别是Rt△AOB和Rt△COD斜边上的中线求得PO=PA、QO=QC,从而得到∠PAO=∠AOP,∠QCO=∠COQ,然后求得QCO=45°,利用解直角三角形求得AC的长即可.
解:(1)![]() 中,
中,![]()
![]() 米,
米,![]() 米,
米,![]() 米
米
![]() (米),
(米),![]() (米),
(米),![]() 米
米
![]() 中,
中,![]()
![]() ,
,
解得![]() (舍去)
(舍去)![]() (米)
(米)
梯子的顶端沿![]() 下滑
下滑![]() 米.
米.
![]() 分别是
分别是![]() 斜边上的中点
斜边上的中点
∴![]()
∴![]() …
…
∴![]()
∵![]()
∴![]() …
…
![]() ,
,
![]() (米).
(米).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目