题目内容
等腰三角形的面积为48cm2，底边上的高为6cm，腰长为________cm．
10
分析：根据面积先求出底边长，再利用勾股定理即可求出．
解答：∵等腰三角形的面积为48cm2，底边上的高为6cm，
∴底边长=16cm，
根据勾股定理，腰长=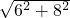
=10cm．
点评：此题主要考查：等腰三角形的“三线合一”的性质和勾股定理的应用．
分析：根据面积先求出底边长，再利用勾股定理即可求出．
解答：∵等腰三角形的面积为48cm2，底边上的高为6cm，
∴底边长=16cm，
根据勾股定理，腰长=
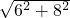=10cm．点评：此题主要考查：等腰三角形的“三线合一”的性质和勾股定理的应用．
练习册系列答案
阅读快车系列答案
相关题目
一次数学课上，老师请同学们在一张长为18厘米，宽为16厘米的矩形纸板上，剪下一个腰长为10厘米的等腰三角形，且要求等腰三角形的一个顶点与矩形的一个顶点重合，其它两个顶点在矩形的边上，则剪下的等腰三角形的面积为多少平方厘米（ ）
| A、50 | B、50或40 | C、50或40或30 | D、50或30或20 |