题目内容
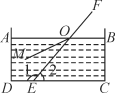
【题目】如图,在平行四边形ABCD中,
(1)以点A为圆心,AB长为半径画弧交AD于点F,再分别以B、F为圆心,大于 ![]() BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF;
BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF;
(2)四边形ABEF是(选填矩形、菱形、正方形、无法确定),说明理由.
【答案】
(1)
解:如图所示;
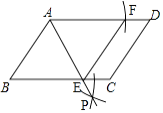
(2)菱形
【解析】菱形,理由如下:
∵在平行四边形ABCD中,AF∥BC,
∴∠FAE=∠AEB,
由(1)知∠BAE=∠FAE,
∴∠BAE=∠AEB,
∴AB=BE,
∵AB=AF,
∴BE=AF,
∴四边形ABEF是菱形,
所以答案是:菱形.
(1)根据要求作图即可;(2)由(1)作图知∠BAE=∠FAE,结合∠FAE=∠AEB得∠BAE=∠AEB,从而得AB=BE,进一步由菱形的判定可得.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

 考前必练系列答案
考前必练系列答案【题目】某中学八年级![]() 班数学课外兴趣小组在探究:“
班数学课外兴趣小组在探究:“![]() 边形共有多少条对角线”这一问题时,设计了如下表格:
边形共有多少条对角线”这一问题时,设计了如下表格:
多边形的边数 |
|
|
|
|
| … |
从多边形一个顶点出发可引起的对角线条数 | … | |||||
多边形对角线的总条数 | … |
![]() 探究:假若你是该小组的成员,请把你研究的结果填入上表;
探究:假若你是该小组的成员,请把你研究的结果填入上表;
![]() 猜想:随着边数的增加,多边形对角线的条数会越来越多,从
猜想:随着边数的增加,多边形对角线的条数会越来越多,从![]() 边形的一个顶点出发可引的对角线条数为多少,
边形的一个顶点出发可引的对角线条数为多少,![]() 边形对角线的总条数为多少.
边形对角线的总条数为多少.
![]() 应用:
应用:![]() 个人聚会,每不相邻的人都握一次手,共握多少次手?
个人聚会,每不相邻的人都握一次手,共握多少次手?
【题目】首都国际机场连续五年排名全球最繁忙机场第二位,该机场2012﹣2016年客流量统计结果如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
客流量(万人次) | 8192 | 8371 | 8613 | 8994 | 9400 |
根据统计表中提供的信息,预估首都国际机场2017年客流量约万人次,你的预估理由是 .