题目内容
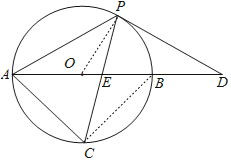
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
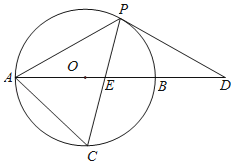
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=2,求CECP的值.
【答案】(1)PD是⊙O的切线,理由见解析;(2)2
【解析】
(1)连结OP,根据圆周角定理可得∠AOP=2∠ACP=120°,然后计算出∠PAD和∠D的度数,进而可得∠OPD=90°,从而证明PD是⊙O的切线;
(2)连结BC,首先求出∠CAB=∠ABC=∠APC=45°,然后可得AC长,再证明△CAE∽△CPA,进而可得![]() ,然后可得CECP的值.
,然后可得CECP的值.
解:(1)如图,PD是⊙O的切线.
理由如下:
连结OP,
∵∠ACP=60°,
∴∠AOP=120°,
∵OA=OP,
∴∠OAP=∠OPA=30°,
∵PA=PD,
∴∠PAO=∠D=30°,
∴∠OPD=90°,
∴PD是⊙O的切线.
(2)连结BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵C为弧AB的中点,
∴∠CAB=∠ABC=∠APC=45°,
∵AB=2,AC=ABsin45°=![]() ,
,
∵∠C=∠C,∠CAB=∠APC,
∴△CAE∽△CPA,
∴![]()
∴![]() =2.
=2.

【题目】某校九年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,数据整理过程如下,请完成下面数据整理中的问题:
(1)收集数据
从甲、乙两个班中各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65;
乙班:90,55,80,70,55,70,95,80,65,70;
(2)整理描述数据
按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m= ,n= ;
(3)分析数据
①若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有 人;
②现从甲班指定的3名学生(1男2女),乙班指定的2名学生(1男1女)中分别抽取1名学生去参加身体素质拓展训练,用树状图或列表法求出抽到的2名同学中恰好是1男1女的概率.