题目内容
 如图,某容器由A、B、C三个长方体组成,其中A、B、C的底面积分别为25平方厘米、10平方厘米、5平方厘米,C的容积是该容器容积的
如图,某容器由A、B、C三个长方体组成,其中A、B、C的底面积分别为25平方厘米、10平方厘米、5平方厘米,C的容积是该容器容积的| 1 | 4 |
(1)求注水的速度x(单位:立方厘米/秒)和A的高度y(单位:厘米);
(2)求注满该容器所需时间及该容器的高度.
分析:(1)根据题目中所给的时间和高度列出一个含有y及x的二元一次方程组,解此方程组可得答案;
(2)根据C的容积和总容积的关系求出C的容积,再求C的高度及注满C的时间,就可以求出注满容器所需时间及容器的高度.
(2)根据C的容积和总容积的关系求出C的容积,再求C的高度及注满C的时间,就可以求出注满容器所需时间及容器的高度.
解答:解:(1)根据题意得,
,
解得
.
答:A的高度是4cm,注水的速度是10cm3/s;
(3)设C的容积为zcm3,由题意得:
4z=10x+8x+z,
将x=10代入计算得:z=60,
那么容器C的高度为:60÷5=12(cm),
故这个容器的高度是:12+12=24(cm),
∵B的注水时间为8s,底面积为10cm2,v=10cm3,
∴B的高度=8×10÷10=8(cm),
注满C的时间是:60÷x=60÷10=6(s),
故注满这个容器的时间为:18+6=24(s).
答:注满容器所需时间为24s,容器的高度为24cm.
|
解得
|
答:A的高度是4cm,注水的速度是10cm3/s;
(3)设C的容积为zcm3,由题意得:
4z=10x+8x+z,
将x=10代入计算得:z=60,
那么容器C的高度为:60÷5=12(cm),
故这个容器的高度是:12+12=24(cm),
∵B的注水时间为8s,底面积为10cm2,v=10cm3,
∴B的高度=8×10÷10=8(cm),
注满C的时间是:60÷x=60÷10=6(s),
故注满这个容器的时间为:18+6=24(s).
答:注满容器所需时间为24s,容器的高度为24cm.
点评:此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,计算出注水速度.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 用了
用了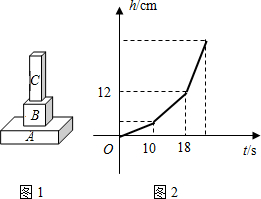 如图1,某容器由A、B、C三个长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是容器容积的
如图1,某容器由A、B、C三个长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是容器容积的 (容器各面的厚
(容器各面的厚
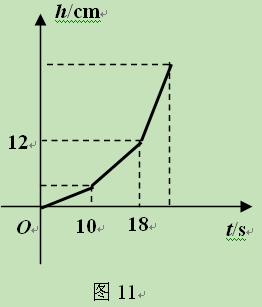
 如图,某容器由A、B、C三个长方体组成,其中A、B、C的底面积分别为25平方厘米、10平方厘米、5平方厘米,C的容积是该容器容积的
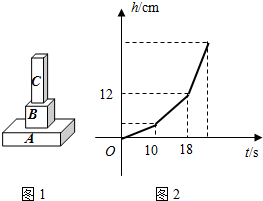
如图,某容器由A、B、C三个长方体组成,其中A、B、C的底面积分别为25平方厘米、10平方厘米、5平方厘米,C的容积是该容器容积的 (容器各面的厚度忽略不计).现以速度x(单位:立方厘米/秒)均匀向容器注水,直至注满为止. 10秒时水位上升至A、B相接处; 18秒时水位上升至B、C相接处,此时水位高为12厘米(即A、B高度和为12厘米).
(容器各面的厚度忽略不计).现以速度x(单位:立方厘米/秒)均匀向容器注水,直至注满为止. 10秒时水位上升至A、B相接处; 18秒时水位上升至B、C相接处,此时水位高为12厘米(即A、B高度和为12厘米).