Question

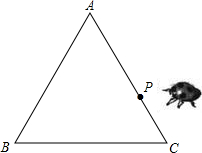如图是一个等边三角形木框，甲虫P在边框AC上爬行（A，C端点除外），设甲虫P到另外两边的距离之和为d，等边三角形ABC的高为h，则d与h的大小关系是（　　）

• A、d＞h
• B、d＜h
• C、d=h
• D、无法确定

Answer 1

分析：如图，连接BP，过点P做PD⊥BC，PE⊥AB，分别交于BC，AB于点D，E，则△ABC分成两个三角形：△BPC和△BPA，根据两三角形面积之和等于等边三角形的面积可推得：d=h．

解答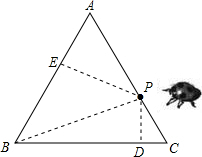：解：如图，连接BP，过点P做PD⊥BC，PE⊥AB，分别交于BC，AB于点D，E，
∴S_△ABC=S_△BPC+S_△BPA=

1

2

BC•PD+

1

2

AB•PE=

1

2

BC•PD+

1

2

BC•PE=

1

2

BC（PD+PE）=

1

2

d•BC=

1

2

h•BC
∴d=h．
故选C．

点评：本题通过作辅助线，把等边三角形分成两部分，利用三角形的面积公式求得d=h．