题目内容
（本小题满分6分）某风景区内有一古塔AB，在塔的北面有一建筑物，当光线与水平面的夹角是30°时，塔在建筑物的墙上留下了高3米的影子CD；而当光线与地面的夹角是45°时，塔尖A在地面上的影子E与墙角C有15米的距离（B、E、C在一条直线上），求塔AB的高度（结果保留根号）．
见解析解析:
如图，过点D作DF⊥AB，垂足为F，∵AB⊥BC，CD⊥BC，
∴四边形BCDF的矩形，∴BC=DF，CD=BF，
设AB=x米，在Rt△ABE中，∠AEB=∠BAE=45°，∴BE=AB=x，
在Rt△ADF中，∠ADF=30°，AF=AB-BF=x-3，∴DF=AF•cot30°=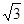
（x-3），
∵DF=BC=BE+EC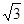，∴（x-3）=x+15，解得x=12+9，
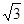答：塔AB的高度（12+9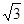）米．
如图，过点D作DF⊥AB，垂足为F，∵AB⊥BC，CD⊥BC，
∴四边形BCDF的矩形，∴BC=DF，CD=BF，
设AB=x米，在Rt△ABE中，∠AEB=∠BAE=45°，∴BE=AB=x，
在Rt△ADF中，∠ADF=30°，AF=AB-BF=x-3，∴DF=AF•cot30°=
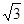（x-3），∵DF=BC=BE+EC，∴
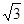（x-3）=x+15，解得x=12+9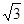，答：塔AB的高度（12+9
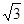）米． 
练习册系列答案
阅读快车系列答案
相关题目
（本小题满分7分）
某中学七年级（8）班同学全部参加课外体育活动情况统计如图：
（1）请你根据以上统计图中的信息，填写下表：
| 该班人数 | 这五个活动项目人数的中位数 | 这五个活动项目人数的平均数 |
|
|
|
|
（2）请你将该条形统计图补充完整
（本小题满分7分）
某中学七年级（8）班同学全部参加课外体育活动情况统计如图：
（1）请你根据以上统计图中的信息，填写下表：
（2）请你将该条形统计图补充完整
某中学七年级（8）班同学全部参加课外体育活动情况统计如图：
（1）请你根据以上统计图中的信息，填写下表：
| 该班人数 | 这五个活动项目人数的中位数 | 这五个活动项目人数的平均数 |
| | | |
且过顶点C（0，5）（长度单位：m）
,求购买地毯需多少元？