题目内容
13、AD，BE，CF是锐角△ABC的三条高．从A引EF的垂线l1，从B引FD的垂线l2，从C引DE的垂线l3．求证：l1，l2，l3三线共点．
分析：设l1、l2交于O点，证明O点为AC中垂线上的点，设l2、l3交于O′点，同理可证O′为BC中垂线上的点，根据三角形的三边中垂线交于一点，可证l1，l2，l3三线共点．
解答：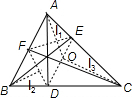
证明：设l1、l2交于O点，
∵∠ADB=∠AEB=90°，
∴A、B、D、E四点共圆，
∴∠BED=∠BAD，
同理，由B、C、E、F四点共圆，得∠BEF=∠BCF，
由互余关系可知∠BAD=∠BCF，
∴∠BEF=∠BED，
又BE⊥AE，l1⊥EF，
∴∠BEF=∠OAE，
同理可证∠BED=∠OCE，∴∠OAE=∠OCE，
∴O点为AC中垂线上的点，
设l2、l3交于O′点，
同理可证O′为BC中垂线上的点，
∵三角形的三边中垂线交于一点（外心），
∴l1，l2，l3三线共点．
证明：设l1、l2交于O点，∵∠ADB=∠AEB=90°，
∴A、B、D、E四点共圆，
∴∠BED=∠BAD，
同理，由B、C、E、F四点共圆，得∠BEF=∠BCF，
由互余关系可知∠BAD=∠BCF，
∴∠BEF=∠BED，
又BE⊥AE，l1⊥EF，
∴∠BEF=∠OAE，
同理可证∠BED=∠OCE，∴∠OAE=∠OCE，
∴O点为AC中垂线上的点，
设l2、l3交于O′点，
同理可证O′为BC中垂线上的点，
∵三角形的三边中垂线交于一点（外心），
∴l1，l2，l3三线共点．
点评：本题考查了四点共圆的判定与性质，圆内接四边形的性质．关键是利用四点共圆的性质，互余关系推出角相等，得到等腰三角形，证明等腰三角形的顶点为三角形三边中垂线上的点，利用外心的性质进行判断．
练习册系列答案
名校课堂系列答案
相关题目