题目内容
已知点F,D,E分别在AB,BC,AC上,AD,BE,CF是锐角△ABC的三条高,AB=6,BC=5,EF=3,则AE= .
【答案】分析:根据题意推出△AEB∽△AFC,即可推出AE:AF=AB:AC,从而推出△AEF∽△ABC,即可求出AE的长度.
解答:解:∵AD,BE,CF是锐角△ABC的三条高,∠BAE=∠FAC,
∴△AEB∽△AFC,
∴AE:AF=AB:AC,
∵∠BAC=∠EAF,
∴△AEF∽△ABC,
∴A:EAB=AF:AC,
∵AB=6,BC=5,EF=3,
∴AE= .
.
故答案为 .
.
点评:本题主要考查相似三角形的判定和性质,关键在于通过推出△AEB∽△AFC,求证∠BAC=∠EAF.
解答:解:∵AD,BE,CF是锐角△ABC的三条高,∠BAE=∠FAC,
∴△AEB∽△AFC,
∴AE:AF=AB:AC,
∵∠BAC=∠EAF,
∴△AEF∽△ABC,
∴A:EAB=AF:AC,
∵AB=6,BC=5,EF=3,
∴AE=
 .
.故答案为
 .
.点评:本题主要考查相似三角形的判定和性质,关键在于通过推出△AEB∽△AFC,求证∠BAC=∠EAF.

练习册系列答案
相关题目

 如图,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且
如图,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且 如图所示,在△ABC中,已知点D,E,F分别为BC,AD,BE的中点.且S△ABC=8cm2,则图中△CEF的面积=
如图所示,在△ABC中,已知点D,E,F分别为BC,AD,BE的中点.且S△ABC=8cm2,则图中△CEF的面积=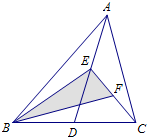 如图,△ABC中,已知点D、E、F分别为BC、AD、CE的中点,设△ABC的面积为S△ABC,△BEF的面积为S△BEF,则S△BEF:S△ABC=
如图,△ABC中,已知点D、E、F分别为BC、AD、CE的中点,设△ABC的面积为S△ABC,△BEF的面积为S△BEF,则S△BEF:S△ABC=