Question

【题目】如果等腰三角形一腰上的高与另一腰的夹角为45°，那么这个等腰三角形的底角度数为 ．

Answer 1

【答案】67.5°或22.5°
【解析】解：有两种情况；（1）如图当△ABC是锐角三角形时，BD⊥AC于D，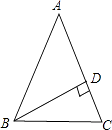
则∠ADB=90°，
已知∠ABD=45°，
∴∠A=90°﹣45°=45°，
∵AB=AC，
∴∠ABC=∠C= ×（180°﹣45°）=67.5°，
2）如图 当△EFG是钝角三角形时，FH⊥EG于H，则∠FHE=90°，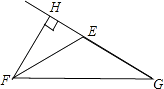

已知∠HFE=45°，
∴∠HEF=90°﹣45°=45°，
∴∠FEG=180°﹣45°=135°，
∵EF=EG，
∴∠EFG=∠G，
= ×（180°﹣135°），
=22.5°．
所以答案是：67.5°或22.5°．
【考点精析】掌握三角形的内角和外角和等腰三角形的性质是解答本题的根本，需要知道三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；等腰三角形的两个底角相等（简称：等边对等角）．