题目内容
(2010•石景山区一模)已知:如图1,等边△ABC为2 ,一边在x上且A(1-
,一边在x上且A(1- ,0),AC交y轴于点,过点E作EF∥AB交BC于点F.
,0),AC交y轴于点,过点E作EF∥AB交BC于点F.(1)直接写出点B、C的坐标;
(2)若直线y=kx-1(k≠0)将四边形EABF的面积等分,求k的值;
(3)如图2,过点A、B、C线与y轴交于点D,M为线段OB上的一个动点,过x轴上一点G(-2,0)作DM的垂线,垂足为H,直线GH交y轴于点N,当M在线段OB上运动时,现给出两个结论:①∠GNM=∠CDM;②∠MGN=∠DCM,其中只有一个是正确的,请你判断哪个结论正确,并证明.

【答案】分析:(1)根据A点的坐标可得OA的长,由等边三角形的边长即可求出OB的长,从而得到B点的坐标;由于C在线段AB的垂直平分线上,根据A、B的坐标,可得C点的横坐标,易求得等边三角形的高,也就求出了C点的坐标.
(2)过C作x轴的垂线,交EF于Q,交AB于P,若直线y=kx-1平分四边形ABFE的面积,那么此直线必过点PQ的中点R(因为分成的两个梯形的上下底之和相同,高相同);在Rt△EOA中,根据∠EAO的度数和OA的长,可求出点E的坐标,进而可求出点Q的坐标,P点的坐标易求得,则可得到点R的坐标,然后将点R代入直线y=kx-1中,即可求出待定系数k的值,从而确定该直线的解析式.
(3)①的结论是正确的;由于OG=OD=2,且GH⊥DM,则可证得△NGO≌△MDO,由此可得∠GNO=∠DMO;而ON=OM(全等三角形的对应边),故∠ONM=45;过D作DT⊥CP于T,根据C、D的坐标可知CT=DT=1,即∠CDT=45°,而∠TDM、∠DMO是平行线DT、AB的内错角,故∠TDM=∠DMO=∠GNO,因此∠TDM、∠GNO都加上45°后仍然相等,即∠GNM=∠CDM.
解答: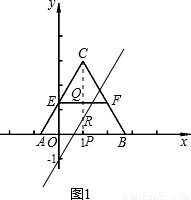 解:(1)易知OA=
解:(1)易知OA=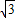 -1,AB=2
-1,AB=2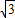 ,
,
故OB=AB-OA=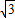 +1;
+1;
易求得等边△ABC的高为:3,
∴B(1+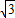 ,0);
,0);
由于C点在线段AB的垂直平分线上,
因此C点的横坐标为:
 (1+
(1+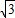 +
+ -1)=1,
-1)=1,
∴C(1,3);
故B(1+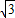 ,0)、C(1,3).(2分)
,0)、C(1,3).(2分)
(2)过点C作CP⊥AB于P,交EF于点Q,取PQ的中点R;
∵△ABC是等边三角形,A(1-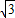 ,0),
,0),
∴∠EAO=60°,
在Rt△EOA中,∠EOA=90°,
∴EO=AO•tan60°=-(1-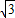 )×
)×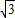 =
=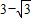 ,
,
∴E(0,3-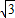 );
);
∵EF∥AB交BC于F,C(1,3),
∴R(1,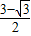 );
);
∵直线y=kx-1将四边形EABF的面积两等分,
∴直线y=kx-1必过点R(1,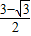 ),
),
∴k-1=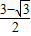 ,
,
∴k=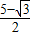 .(4分)
.(4分)
(3)正确结论:①∠GNM=∠CDM,
证明:可求得过A、B、C的抛物线解析式为y=-x2+2x+2;(5分)
∴D(0,2),
∵G(-2,0),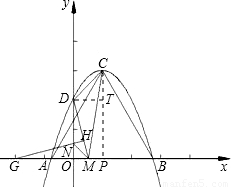
∴OG=OD,
由题意∠GON=∠DOM=90°,
又∵∠GNO=∠DNH,
∴∠NGO=∠MDO,
∴△NGO≌△MDO,
∴∠GNO=∠DMO,OM=ON,
∴∠ONM=∠NMO=45°,
过点D作DT⊥CP于T;
∴DT=CT=1,
∴∠CDT=∠DCT=45°,
由题意可知DT∥AB,
∴∠TDM=∠DMO,
∴∠TDM+45°=∠DMO+45°=∠GNO+45°,
∴∠TDM+∠CDT=∠GNO+∠ONM,
即:∠GNM=∠CDM.(7分)
点评:此题考查了等边三角形的性质、图形面积的求法、函数解析式的确定、全等三角形及等腰直角三角形的判定和性质等知识,综合性强,难度较大.
(2)过C作x轴的垂线,交EF于Q,交AB于P,若直线y=kx-1平分四边形ABFE的面积,那么此直线必过点PQ的中点R(因为分成的两个梯形的上下底之和相同,高相同);在Rt△EOA中,根据∠EAO的度数和OA的长,可求出点E的坐标,进而可求出点Q的坐标,P点的坐标易求得,则可得到点R的坐标,然后将点R代入直线y=kx-1中,即可求出待定系数k的值,从而确定该直线的解析式.
(3)①的结论是正确的;由于OG=OD=2,且GH⊥DM,则可证得△NGO≌△MDO,由此可得∠GNO=∠DMO;而ON=OM(全等三角形的对应边),故∠ONM=45;过D作DT⊥CP于T,根据C、D的坐标可知CT=DT=1,即∠CDT=45°,而∠TDM、∠DMO是平行线DT、AB的内错角,故∠TDM=∠DMO=∠GNO,因此∠TDM、∠GNO都加上45°后仍然相等,即∠GNM=∠CDM.
解答:
 解:(1)易知OA=
解:(1)易知OA=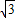 -1,AB=2
-1,AB=2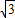 ,
,故OB=AB-OA=
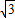 +1;
+1;易求得等边△ABC的高为:3,
∴B(1+
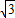 ,0);
,0);由于C点在线段AB的垂直平分线上,
因此C点的横坐标为:
 (1+
(1+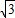 +
+ -1)=1,
-1)=1,∴C(1,3);
故B(1+
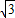 ,0)、C(1,3).(2分)
,0)、C(1,3).(2分)(2)过点C作CP⊥AB于P,交EF于点Q,取PQ的中点R;
∵△ABC是等边三角形,A(1-
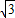 ,0),
,0),∴∠EAO=60°,
在Rt△EOA中,∠EOA=90°,
∴EO=AO•tan60°=-(1-
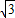 )×
)×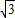 =
=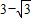 ,
,∴E(0,3-
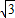 );
);∵EF∥AB交BC于F,C(1,3),
∴R(1,
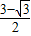 );
);∵直线y=kx-1将四边形EABF的面积两等分,
∴直线y=kx-1必过点R(1,
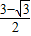 ),
),∴k-1=
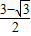 ,
,∴k=
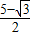 .(4分)
.(4分)(3)正确结论:①∠GNM=∠CDM,
证明:可求得过A、B、C的抛物线解析式为y=-x2+2x+2;(5分)
∴D(0,2),
∵G(-2,0),

∴OG=OD,
由题意∠GON=∠DOM=90°,
又∵∠GNO=∠DNH,
∴∠NGO=∠MDO,
∴△NGO≌△MDO,
∴∠GNO=∠DMO,OM=ON,
∴∠ONM=∠NMO=45°,
过点D作DT⊥CP于T;
∴DT=CT=1,
∴∠CDT=∠DCT=45°,
由题意可知DT∥AB,
∴∠TDM=∠DMO,
∴∠TDM+45°=∠DMO+45°=∠GNO+45°,
∴∠TDM+∠CDT=∠GNO+∠ONM,
即:∠GNM=∠CDM.(7分)
点评:此题考查了等边三角形的性质、图形面积的求法、函数解析式的确定、全等三角形及等腰直角三角形的判定和性质等知识,综合性强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与直线y=
与直线y= x+b交于点A(-3,0)、点B,与y轴交于点C.
x+b交于点A(-3,0)、点B,与y轴交于点C.


