题目内容
(2010•石景山区二模)已知关于x的一元二次方程x2-(m-1)x+m-3=0.(1)求证:不论m取何值时,方程总有两个不相等的实数根.
(2)若直线y=(m-1)x+3与函数y=x2+m的图象C1的一个交点的横坐标为2,求关于x的一元二次方程x2-(m-1)x+m-3=0的解.
(3)在(2)的条件下,将抛物线y=x2-(m-1)x+m-3绕原点旋转180°,得到图象C2,点P为x轴上的一个动点,过点P作x轴的垂线,分别与图象C1、C2交于M、N两点,当线段MN的长度最小时,求点P的坐标.

【答案】分析:(1)证明方程总有两个不相等的实数根,也就是证明判别式恒大于0
(2)将两函数联立,求出m即可,
(3)利用二次函数旋转180°后,系数之间的关系,得出新函数的解析式,在表示出M,N的坐标,即可解决.
解答:(1)证明:△=[-(m-1)]2-4(m-3)=m2-2m+1-4m+12=m2-6m+13=(m-3)2+4,
∵不论m取何值时,(m-3)2≥0,
∴(m-3)2+4>0,即△>0,
∴不论m取何值时,方程总有两个不相等的实数根;
(2)解:将x=2代入方程x2-(m-1)x+m-3=0,得m=3,
再将m=3代入,原方程化为x2-2x=0,
解得x1=0,x2=2.
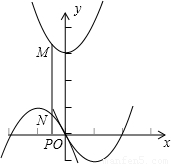
(3)解:将m=3代入得抛物线:y=x2-2x,将抛物线y=x2-2x绕原点旋转180°得到的图象C2的解析式为:y=-x2-2x.设P(x,0),
则M(x,x2+3),N(x,-x2-2x),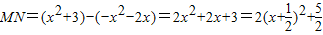 ,
,
∴当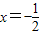 时,MN的长度最小,此时点P的坐标为
时,MN的长度最小,此时点P的坐标为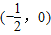 .
.
点评:此题主要考查了一元二次方程的判别式,以及一次函数与二次函数的综合应用,还有二次函数的旋转等,题目综合性较强.
(2)将两函数联立,求出m即可,
(3)利用二次函数旋转180°后,系数之间的关系,得出新函数的解析式,在表示出M,N的坐标,即可解决.
解答:(1)证明:△=[-(m-1)]2-4(m-3)=m2-2m+1-4m+12=m2-6m+13=(m-3)2+4,
∵不论m取何值时,(m-3)2≥0,
∴(m-3)2+4>0,即△>0,
∴不论m取何值时,方程总有两个不相等的实数根;
(2)解:将x=2代入方程x2-(m-1)x+m-3=0,得m=3,
再将m=3代入,原方程化为x2-2x=0,
解得x1=0,x2=2.
(3)解:将m=3代入得抛物线:y=x2-2x,将抛物线y=x2-2x绕原点旋转180°得到的图象C2的解析式为:y=-x2-2x.设P(x,0),
则M(x,x2+3),N(x,-x2-2x),
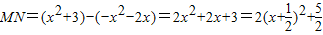 ,
,∴当
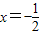 时,MN的长度最小,此时点P的坐标为
时,MN的长度最小,此时点P的坐标为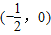 .
.
点评:此题主要考查了一元二次方程的判别式,以及一次函数与二次函数的综合应用,还有二次函数的旋转等,题目综合性较强.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 与直线y=
与直线y= x+b交于点A(-3,0)、点B,与y轴交于点C.
x+b交于点A(-3,0)、点B,与y轴交于点C.

 ,一边在x上且A(1-
,一边在x上且A(1- ,0),AC交y轴于点,过点E作EF∥AB交BC于点F.
,0),AC交y轴于点,过点E作EF∥AB交BC于点F.
