题目内容
【题目】如图，在
中，
，
，
平分
，
是
中点，则下列结论正确的个数为（ ）
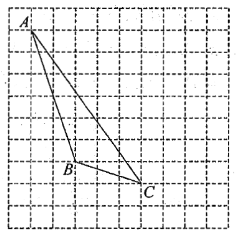
（1）
（2）
（3）
（4）
A. 1B. 2C. 3D. 4
【答案】D
【解析】
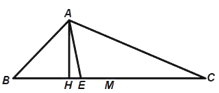
（1）延长AB取BD=BE，连接DE，由∠D=∠BED，
，得到∠D=∠C，在△ADE和△ACE中，利用AAS证明
，可得AC=AD=AB+BE；
（2）在HC上截取HF=BH,连接AF，可知△ABF为等腰三角形，再根据
，可得出△AFC为等腰三角形，所以FC+BH+HF=AB+2BH=BC；
（3）HM=BM-BH，所以2HM=2BM-2BH=BC-2BH，再结合（2）中结论，可得
；
（4）结合（1）（2）的结论，
.
解：
①延长AB取BD=BE，连接DE，
∴∠D=∠BED，∠ABC=∠D+∠BED=2∠D,
∵，∴∠D=∠C，
在△ADE和△ACE中，
，
∴
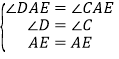∴AC=AD=AB+BE，故（1）正确；
②在HC上截取HF=BH,连接AF，
∵
，∴△ABF为等腰三角形，
∴AB=AF，∠ABF=∠AFB，
∵，∴∠AFB=2∠C=∠C+∠CAF，
∴FC=AF=AB，
∴FC+BH+HF=AB+2BH=BC，
故（2）正确；
③
∵HM=BM-BH，∴2HM=2BM-2BH=BC-2BH，
由②可知BC-2BH=AB，
∴
④
根据①②结论，可得:
，
故（4）正确；
故选D.
练习册系列答案
相关题目
