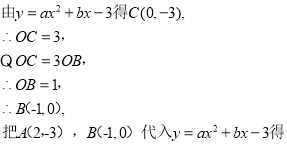��Ŀ����
����Ŀ���ۺ���̽��
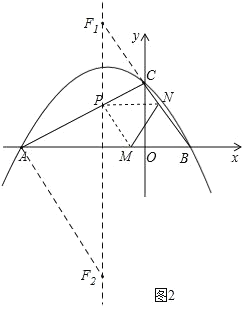
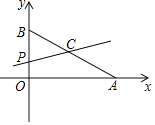
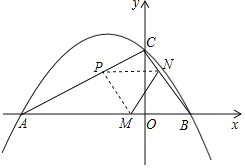
��ͼ��������y��ax2+bx+c��a��0����x�ύ��A����3��0����B���㣬��y���ཻ�ڵ�![]() ����x����4��x��2ʱ�����κ���y��ax2+bx+c��a��0���ĺ���ֵy��ȣ�����AC��BC��
����x����4��x��2ʱ�����κ���y��ax2+bx+c��a��0���ĺ���ֵy��ȣ�����AC��BC��
��1���������ߵĽ���ʽ��
��2���жϡ�ABC����״����˵�����ɣ�
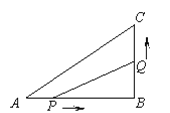
��3������M��Nͬʱ��B�����������ÿ��1����λ���ȵ��ٶȷֱ���BA��BC���˶�������һ���㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt��ʱ������MN������BMN��MN���ۣ�B��ǡ������AC���ϵ�P������t��ֵΪ�� ������P������Ϊ�� ����
��4�������߶Գ������Ƿ����һ��F��ʹ�á�ACF����ACΪֱ�DZߵ�ֱ�������Σ��������ڣ���˵�����ɣ������ڣ���ֱ��д����F�����꣮
���𰸡���1��![]() ����2����ABC��ֱ�������Σ����ɼ���������3��
����2����ABC��ֱ�������Σ����ɼ���������3��![]() ��
��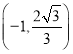 ����4�����ڣ�F1
����4�����ڣ�F1![]() ��F2
��F2![]() ��
��
��������
��1���ɶԳ����������B�����꣬���������ߵĽ���ʽΪy=a(x+3)(x��1)����C�������y=a(x+3)(x��1)���ɣ�
��2�����жϡ�ABCΪֱ�������Σ��ֱ����AB��AC��BC�ij����ɹ��ɶ������涨����֤�����ۣ�
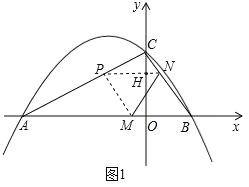
��3����Ϊ��M��Nͬʱ��B�����������ÿ��1����λ���ȵ��ٶȷֱ���BA��BC���˶�������BM=BN=t��֤�ı���PMBN�����Σ���PM��y�ύ��H��֤��CPN�ס�CAB�������������ε����ʿ����t��ֵ��CH�ij����ɵó���P�����꣬���ֱ��AC�Ľ���ʽ������P��������뼴�ɣ�
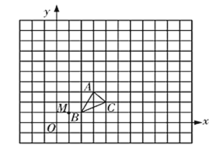
��4�����ֱ��BC�Ľ���ʽ����ͼ2������ACF=90��ʱ����B��C��F��һ��ֱ���ϣ����ֱ��BC��Գ���Ľ��㼴�ɣ�����CAF=90��ʱ�����ֱ��AF�Ľ���ʽ����������Գ���Ľ��㼴�ɣ�
��1������������y=ax2+bx+c�У���x=��4��x=2ʱ�����κ���y=ax2+bx+c�ĺ���ֵy��ȣ�
�������ߵĶԳ���Ϊx![]() 1��
1��
�֡�������y=ax2+bx+c��x�ύ��A(��3��0)��B���㣬
�ɶԳ��Կ�֪B(1��0)��
����������ߵĽ���ʽΪy=a(x+3)(x��1)��
��C(0��![]() )����y=a(x+3)(x��1)��
)����y=a(x+3)(x��1)��
���3a![]() ��
��
��ã�a![]() ��
��
��������ߵĽ���ʽΪy![]() (x+3)(x��1)
(x+3)(x��1)![]() x2
x2![]() x
x![]() ��
��
��2����ABCΪֱ�������Σ��������£�
��A(��3��0)��B(1��0)��C(0��![]() )��
)��
��OA=3��OB=1��OC![]() ��
��
��AB=OA+OB=4��AC![]() 2
2![]() ��BC
��BC![]() 2��
2��
��AC2+BC2=16��AB2=16��
��AC2+BC2=AB2��
���ABC��ֱ�������Σ�
��3���ߵ�M��Nͬʱ��B�����������ÿ��1����λ���ȵ��ٶȷֱ���BA��BC���˶���
��BM=BN=t��
�ɷ���֪����BMN�ա�PMN��
��BM=PM=BN=PN=t��
���ı���PMBN�����Σ�
��PN��AB��
���CPN�ס�CAB����PM��y�ύ��H��
��![]() ��
��
��![]() ��
��
��ã�t![]() ��CH
��CH![]() ��
��
��OH=OC��CH![]() ��
��
��yP![]() ��
��
��ֱ��AC�Ľ���ʽΪy=kx![]() ��
��
����A(��3��0)����y=kx![]() ��
��
�ã�k![]() ��
��
��ֱ��AC�Ľ���ʽΪy![]() x
x![]() ��
��
��yP![]() ����y
����y![]() x
x![]() ��
��
��x=��1��
��P(��1��![]() )��
)��
�ʴ�Ϊ��![]() ��(��1��
��(��1��![]() )��
)��
��4����ֱ��BC�Ľ���ʽΪy=kx![]() ��
��
����B(1��0)����y=kx![]() ��
��
�ã�k![]() ��
��
��ֱ��BC�Ľ���ʽΪy![]() x
x![]() ��
��
�ɣ�2��֪��ABCΪֱ�������Σ���ACB=90�㣮
����ͼ2������ACF=90��ʱ����B��C��F��һ��ֱ���ϣ�
��y![]() x
x![]() �У���x=��1ʱ��y=2
�У���x=��1ʱ��y=2![]() ��
��
��F1(��1��2![]() )��
)��
�ڵ���CAF=90��ʱ��AF��BC��
�����ֱ��AF�Ľ���ʽΪy![]() x+n��
x+n��
����A(��3��0)����y![]() x+n��
x+n��
�ã�n=��3![]() ��
��
��ֱ��AF�Ľ���ʽΪy![]() x��3
x��3![]() ��
��
��y![]() x��3
x��3![]() �У���x=��1ʱ��y=��2
�У���x=��1ʱ��y=��2![]() ��
��
��F2(��1����2![]() )��
)��
������������F������ΪF1(��1��2![]() )��F2(��1����2
)��F2(��1����2![]() )��
)��