题目内容
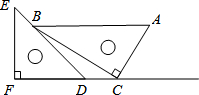 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD=
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD=15-5
| 3 |
15-5
.| 3 |
分析:过点B作BM⊥FD于点M,根据题意可求出BC的长度,然后在△EFD中可求出∠EDF=45°,进而可得出答案.
解答: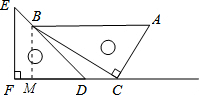 解:过点B作BM⊥FD于点M,
解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=10×tan60°=10
,
∵AB∥CF,
∴BM=BC×sin30°=10
×
=5
,
CM=BC×cos30°=15,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5
,
∴CD=CM-MD=15-5
.
故答案是:15-5
.
 解:过点B作BM⊥FD于点M,
解:过点B作BM⊥FD于点M,在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=10×tan60°=10
| 3 |
∵AB∥CF,
∴BM=BC×sin30°=10
| 3 |
| 1 |
| 2 |
| 3 |
CM=BC×cos30°=15,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5
| 3 |
∴CD=CM-MD=15-5
| 3 |
故答案是:15-5
| 3 |
点评:本题考查了解直角三角形的性质及平行线的性质,难度较大,解答此类题目的关键根据题意建立三角形利用所学的三角函数的关系进行解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 一副直角三角板如图放置,点C在FD的延长线上,已知AB∥FC,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=8,则CD的长为
一副直角三角板如图放置,点C在FD的延长线上,已知AB∥FC,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=8,则CD的长为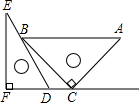 (2012•巴中)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12
(2012•巴中)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的余角的度数是
将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的余角的度数是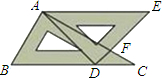 将一副直角三角板如图放置,己知∠AFD=75°,AE和BC平行吗?请说明理由.
将一副直角三角板如图放置,己知∠AFD=75°,AE和BC平行吗?请说明理由.