题目内容
下表给出的是关于一次函数y=kx+b的自变量x及其对应的函数值y的若干信息：则根据表格中的相关数据可以计算得到m的值是（ ）
|
分析：设一次函数解析式为y=kx+b（k≠0），将（-1，0）、（0，1）、（1，m）代入即可得出答案．
解答：解：设一次函数解析式为：y=kx+b（k≠0）．
根据图示知，该一次函数经过点（-1，0）、（0，1），则
，
解得，
；
∴该一次函数的解析式为y=x+1：
又∵该一次函数经过点（1，m），
∴m=1+1=2，即m=2；
故选C．
根据图示知，该一次函数经过点（-1，0）、（0，1），则
|
解得，
|
∴该一次函数的解析式为y=x+1：
又∵该一次函数经过点（1，m），
∴m=1+1=2，即m=2；
故选C．
点评：本题考查待定系数法求函数解析式的知识，比较简单，注意掌握待定系数法的运用．
练习册系列答案
相关题目
；
．
．
．
； 
阅读下列解题过程，借鉴其中一种方法解答后面给出的试题：
问题：某人买13个鸡蛋，5个鸭蛋、9个鹅蛋共用去了9.25元；买2个鸡蛋，4个鸭蛋、3个鹅蛋共用去了3.20元．试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元．
分析：设买鸡蛋，鸭蛋、鹅蛋各一个分别需x、y、z元，则需要求x+y+z的值．由题意，知
；
视
为常数，将上述方程组看成是关于y、z的二元一次方程组，化“三元”为“二元”、化“二元”为“一元”从而获解．
解法1：视为常数，依题意得
解这个关于y、z的二元一次方程组得
于是
．
评注：也可以视z为常数，将上述方程组看成是关于、
的二元一次方程组，解答方法同上，你不妨试试．
分析：视
为整体，由(1)、(2)恒等变形得
，
．
解法2：设
，
，代入(1)、(2)可以得到如下关于
、
的二元一次方
程组
由⑤+4×⑥，得
，
．
评注：运用整体的思想方法指导解题．视，
为整体，令
，
，代人①、②将原方程组转化为关于、的二元一次方程组从而获解．
请你运用以上介绍的任意一种方法解答如下数学竞赛试题：
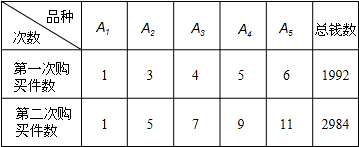
购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表：
|
次数 | A1 | A2 | A3 | A4 | A5 | 总钱数 |
| 第一次购 买件数 | l | 3 | 4 | 5 | 6 | 1992 |
| 第二次购 买件数 | l | 5 | 7 | 9 | 11 | 2984 |
品名那么，购买每种教学用具各一件共需多少元?
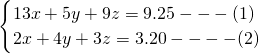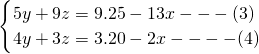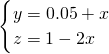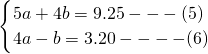